Spiral
En spiral är en speciell kurva inom matematiken. Denna kurva börjar vid en punkt och går sedan runt denna punkt, men kommer längre och längre bort från den. Detta skiljer sig från en cirkel (som alltid är på samma avstånd) eller en ellips. En spiral är en "öppen" kurva, till skillnad från cirklar och ellipser som är slutna kurvor.

Utsnitt av ett nautilusskal som visar kamrarna i en ungefär logaritmisk spiral.
Tvådimensionella spiraler
En tvådimensionell spiral kan enklast beskrivas med hjälp av polarkoordinater. Där är radien r en kontinuerlig monoton funktion av vinkeln θ (theta). Cirkeln skulle betraktas som ett degenererat fall. Med cirkeln skulle funktionen inte vara strikt monoton, utan konstant.
Några av de viktigaste typerna av tvådimensionella spiraler är:
- Den arkimediska spiralen: r = a + bθ
- Euler-spiralen, Cornu-spiralen eller clothoiden
- Fermats spiral: r = θ1/2
- Den hyperboliska spiralen: r = a/θ
- Lituus: r = θ-1/2
- Den logaritmiska spiralen: r = abθ ; approximationer av denna finns i naturen.
- Fibonacci-spiralen och den gyllene spiralen: specialfall av den logaritmiska spiralen.
- Theodorus spiral: en approximation av den arkimediska spiralen som består av sammanhängande rätvinkliga trianglar.
· 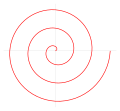
Archimedisk spiral
· 
Cornu spiral
· 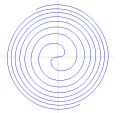
Fermats spiral
· 
hyperbolisk spiral
· 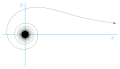
lituus
· 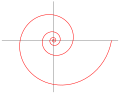
logaritmisk spiral
· 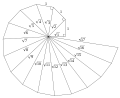
spiral av Theodorus
Tredimensionella spiraler
För enkla tredimensionella spiraler är en tredje variabel, h (höjd), också en kontinuerlig, monoton funktion av θ. Till exempel kan en konisk spiral definieras som en spiral på en konisk yta, där avståndet till toppen är en exponentialfunktion av θ.
Helixen och virveln kan ses som ett slags tredimensionell spiral.
För en spiral med tjocklek, se fjäder (matematik).
I naturen
Studiet av spiraler i naturen har en lång historia, Christopher Wren upptäckte att många snäckor bildar en logaritmisk spiral. Jan Swammerdam observerade de gemensamma matematiska egenskaperna hos ett stort antal skal från Helix till Spirula, och Henry Nottidge Moseley beskrev matematiken hos enskaliga skal. D'Arcy Wentworth Thompsons bok On Growth and Form behandlar utförligt dessa spiraler. Han beskriver hur skal bildas genom att rotera en sluten kurva runt en fast axel. Kurvans form förblir fast men dess storlek växer i en geometrisk progression. I vissa skal, som Nautilus och ammoniter, roterar den genererande kurvan i ett plan som är vinkelrätt mot axeln och skalet bildar en plan skivform. Hos andra följer den en skev bana och bildar ett spiralformigt mönster.
Thompson studerade också spiraler som förekommer i horn, tänder, klor och växter.
Spiraler i växter och djur beskrivs ofta som virvlar.
H Vogel föreslog en modell för mönstret av blomblad i solrosans huvud. Denna modell har följande form
θ = n × 137,5 ∘ , r = c n {\displaystyle \theta =n\ gånger 137,5^{\circ },\ r=c{\sqrt {n}}}
där n {\displaystyle n}

Spiralen representerar också oändligheten. Den utgår från en enda punkt och roterar utåt till universums slut. På grund av detta tror vissa civilisationer att spiralen är en väg till livet efter döden.

Den 53:e tavlan från Ernst Haeckels Kunstformen der Natur (1904), som visar organismer som klassificeras som Prosobranchia (nu kända för att vara polyfyletiska).
Som en symbol
Spiralen spelar en viktig roll i symboliken. Den förekommer i megalitkonst, särskilt i graven i Newgrange och i många galiciska hällristningar, till exempel den i Mogor. Se även trippelspiral.
Forskare talar fortfarande om ämnet, men många av dem tror nu att den enkla spiralen i kinesisk konst kan vara en symbol för solen. Takpannor från Tangdynastin med denna symbol har hittats väster om den antika staden Chang'an (dagens Xian).
Spiralen är den äldsta symbolen som finns på alla civiliserade kontinenter. Eftersom den förekommer på gravplatser över hela världen representerar spiralen troligen cykeln "liv-död-återfödelse". På samma sätt symboliserade spiralen solen, eftersom forntida människor trodde att solen föddes varje morgon, dog varje natt och återföddes nästa morgon.
Spiraler är också en symbol för hypnos. Detta kommer troligen från klyschan med människor och tecknade figurer som hypnotiseras genom att stirra in i en snurrande spiral (ett exempel är Kaa i Disneys Djungelboken). De används också som en symbol för yrsel, där ögonen på en tecknad figur, särskilt i anime och manga. Spiralen symboliserar DNA:s dubbelspiralstruktur, som representerar den biologiska evolutionen, och spiralstrukturen i en galax.

Ingångsplattan i Newgrange
Sök
