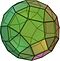
Arkimediska polyeder – definition, egenskaper och historia

Upptäck arkimediska polyeder: definition, historia och unika egenskaper hos de 13–15 polyedrarna med regelbundna ytor — från Arkimedes till Kepler.

Författare: Leandro Alegsa

11-01-2026 02:15

Inom geometrin är en arkimedisk polyeder en konvex polyeder med följande egenskaper:

Varje yta är en regelbunden polygon (många kan förekomma).
Alla hörn (vertex) ser likadana ut: samma typ och ordning av kanter och ytor möts i varje hörn. Detta kallas vertex‑transitivitet.
Formen är varken en platonisk solid, ett prisma eller ett antiprisma.

En viktig följd av definitionen är att en arkimedisk polyeder måste ha minst två olika slags polygoner som ytor — om alla ytor var likadana skulle formen vara en platonisk solid. För att konstruera en arkimedisk solid används ofta operationer som trunkering (avkapning av hörn), kantavplaning (cantellation) eller snubbing (en sorts vridning) av platoniska eller andra symmetriska polyedrar.

Beroende på hur man räknar dem finns det antingen tretton eller femton sådana former. Orsaken till skillnaden är att två av arkimediska solider förekommer i två spegelbilder som inte kan göras kongruenta genom rotation (de är chirala). Dessa två chirala exempel är snub cube och snub dodecahedron; räknar man spegelparen som olika får man 15 varianter, annars 13.

Arkimediska polyeder är uppkallade efter den antika grekiska matematikern Arkimedes, som troligen studerade dem på 300‑talet f.Kr. Arkimedes egna skrifter om detta är förlorade, men deras innehåll återger Pappus av Alexandria i sina sammanställningar på 300–400‑talet e.Kr. Under renässansen återupptäckte både konstnärer och matematiker intresset för dessa "rena former" (rena former) och undersökte deras konstruktioner. Arbetet med att lista och förstå dem avslutades i praktiken av Johannes Kepler omkring 1620; senare gavs formella bevis och fullständig klassificering under 1800‑ och 1900‑talen.

Praktiska exempel och betydelse:

Truncated icosahedron (avskuren ikosaeder) är välkänd som mönstret på en traditionell fotboll och som formen på buckminsterfullerenet C60.
Arkimediska polyeder används inom konst, arkitektur, kristallografi och kemi (molekylgeometrier och nanopartiklar).
Dualerna till de arkimediska soliderna kallas för Catalan‑polyedrar; dessa är face‑transitiva (alla ytor är likadana) men inte vertex‑transitiva.

Exempel på arkimediska polyeder (de 13, om man räknar spegelbilder som samma):

Truncated tetrahedron
Cuboctahedron
Truncated cube
Truncated octahedron
Rhombicuboctahedron
Truncated cuboctahedron (även kallad great rhombicuboctahedron)
Snub cube
Icosidodecahedron
Truncated dodecahedron
Truncated icosahedron
Rhombicosidodecahedron
Truncated icosidodecahedron (även kallad great rhombicosidodecahedron)
Snub dodecahedron

Sammanfattningsvis kännetecknas arkimediska polyeder av hög grad av symmetri (alla hörn likadana) och regelbundna polygonytor, men de är inte helt reguljära eftersom ytorna kan vara olika typer. De kan konstrueras från platoniska och andra reguljära polyedrar genom geometriska operationer och har både teoretiskt och praktiskt värde inom flera vetenskapsområden.

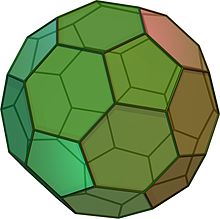
En avtrubbad isosaeder ser ut som en fotboll. Den består av 12 liksidiga femhörningar och 20 regelbundna sexhörningar. Den har 60 hörn och 90 kanter. Den är en arkeimedisk fast kropp.

Egenskaper

Archimediska solider består av regelbundna polygoner, därför har alla kanter samma längd.
Alla arkimediska solider kan framställas från platoniska solider genom att "skära av kanterna" på de platoniska soliderna.
Den typ av polygoner som möts i ett hörn ("vertex") kännetecknar både den arkeimediska och den platonska soliden.

Samband med platonska solider

Platonska solider kan förvandlas till arkimediska solider genom att följa en rad regler för deras konstruktion.

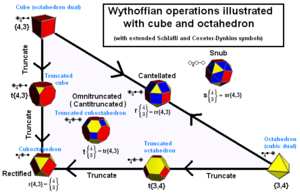
Archimedeans solider kan konstrueras som generatorpositioner i ett kalejdoskop.

Förteckning över arkimediska solider

Följande är en förteckning över alla arkimmediska solider

Bild	Namn	Ansikten	Typ	Kanter	Vertikaler
	Avtrubbad tetraeder	8	4 trianglar 4 hexagonaler	18	12
	Kuboktaeder	14	8 trianglar 6 rutor	24	12
	Avkapad kub	14	8 trianglar 6 åtthörningar	36	24
	Avtrubbad oktaedron	14	6 rutor 8 hexagoner	36	24
	Rhombikuboktaeder	26	8 trianglar 18 rutor	48	24
	Avtrubbad kuboktaeder	26	12 rutor 8 hexagoner 6 åtthörningar	72	48
	Snub cube (2 speglade versioner)	38	32 trianglar 6 rutor	60	24
	Icosidodekaeder	32	20 trianglar 12 femhörningar	60	30
	Avtrubbad dodekaeder	32	20 trianglar 12 decagoner	90	60
	Avtrubbad icosaeder	32	12 femhörningar 20 hexagoner	90	60
	Rhombicosidodekahedron	62	20 trianglar30 fyrkanter12 femhörningar	120	60
	Avtrubbad icosidodekaeder	62	30 rutor 20 hexagoner 12 decagoner	180	120
	Snub dodekahedron (2 speglade versioner)	92	80 trianglar 12 femhörningar	150	60

Frågor och svar

F: Vad är en arkiimedisk solid?

S: En arkimedisk solid är en konvex form av polygoner som har egenskaperna att varje yta är en regelbunden polygon, att alla hörn ser likadana ut och att den inte är en platonisk solid, ett prisma eller ett antiprisma.

Fråga: Hur många arkiedeiska solider finns det?

S: Beroende på hur man räknar dem finns det antingen tretton eller femton arkimediska solider.

Fråga: Vem upptäckte de arkimediska soliderna?

S: De arkimediska soliderna är uppkallade efter den grekiske matematikern Archimedes som troligen upptäckte dem på 300-talet f.Kr.

Fråga: Vad gjorde Pappus av Alexandria med Archimedes skrifter?

S: Pappus av Alexandria sammanfattade Archimedes skrifter om de arkimediska soliderna på 400-talet.

F: Varför återupptäckte konstnärer och matematiker de arkimediska soliderna under renässansen?

S: Under renässansen värderade konstnärer och matematiker rena former, och de arkimediska soliderna ansågs vara rena former.

F: När avslutade Johannes Kepler sökandet efter alla arkimediska solider?

S: Johannes Kepler slutförde troligen sökandet efter alla arkimediska solider omkring 1620.

F: Vad krävs för att konstruera en arkiimedisk solida?

S: För att konstruera en arkimedisk solida krävs minst två olika polygoner.

Sök