Magnetiskt dipolmoment — definition och förklaring

Förstå magnetiskt dipolmoment: tydlig definition, fysik, riktning och hur det påverkar magnetfältet. Enkel förklaring och praktiska exempel.

Författare: Leandro Alegsa

26-02-2026 12:11

Magnetens magnetiska moment är en storhet som bestämmer den kraft som magneten kan utöva på elektriska strömmar och det vridmoment som ett magnetfält utövar på den. En elektrisk strömslinga, en stavmagnet, en elektron, en molekyl och en planet har alla magnetiska moment.

Både det magnetiska momentet och magnetfältet kan betraktas som vektorer med storlek och riktning. Det magnetiska momentets riktning pekar från magnetens syd- till nordpol. Det magnetfält som en magnet producerar är också proportionellt mot dess magnetiska moment. Närmare bestämt avser termen magnetiskt moment normalt ett systems magnetiska dipolmoment, som ger upphov till den första termen i multipolutvidgningen av ett allmänt magnetfält. Dipolkomponenten i ett föremåls magnetfält är symmetrisk i förhållande till riktningen för dess magnetiska dipolmoment och minskar som den omvända kuben av avståndet från föremålet.

Definition och enkel formel

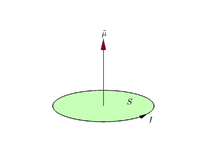
För en plan spole med ström I och area A definieras magnetiskt dipolmoment m (vektor) som

m = I · A · n, där n är enhetsvektorn normalt mot spolen enligt högerhandsregeln (riktningen som ger nordpolens riktning).
För en spole med N varv blir m = N I A.

Enhet i SI är ampere·kvadratmeter (A·m²) vilket också motsvarar joule per tesla (J/T).

Magnetfält från en dipol (i vakuum)

Det magnetiska fältet B från ett magnetiskt dipolmoment m i punkten r (vinkelrätt riktning från dipolen) uttrycks i SI som

B(r) = (μ0 / 4π) · [ (3 (m·r̂) r̂ − m) / r³ ]

där μ0 är vakuumpermeabiliteten (μ0 ≈ 4π·10⁻⁷ N/A²), r̂ är enhetsvektorn från dipolen till observationspunkten och r avståndet. Detta fält avtar som 1/r³ och beskriver långt från källan den dominerande termen i multipolutvidgningen.

Krafter, vridmoment och potentiell energi

Vridmoment: En magnetisk dipol i ett magnetfält B utsätts för vridmoment τ = m × B. I ett homogent fält uppstår ingen netto-kraft, endast ett vridande moment som försöker alignera m med B.
Potentiell energi: U = −m · B. Systemet får lägst energi när m är parallellt och i samma riktning som B.
Kraft i icke-homogent fält: Om fältet varierar i rummet får dipolen en kraft F = ∇(m·B). Detta utnyttjas i exempelvis magnetiska fällor för partiklar och i praktiska instrument.

Atomära och kvantmekaniska magnetiska moment

I atomer och fria partiklar uppstår magnetiska moment från laddade partiklar i rörelse (orbitalt) och från partiklar med spinn (intrinsic). För en elektron gäller ofta relationen

μ = −g (e / 2 m_e) S

där S är spinnvektorn, g är g-faktorn (för elektron nära 2, exakt ≈ 2.0023) och Bohrs magneton μ_B = e ħ / (2 m_e) ≈ 9.274 × 10⁻²⁴ A·m² är en naturlig enhet för elektronens magnetiska moment. I kvantmekanik är magnetiska moment operatorer och har diskreta värden beroende på kvanttalen.

Makroskopiska magnetiska moment och magnetisering

För ett makroskopiskt material definieras magnetisering M (A/m) som det magnetiska dipolmomentet per volymsenhet. Total magnetiskt moment m för ett homogent magnetiserat objekt på volym V är

m = ∫ M dV ≈ M · V (för homogen M).

I ferromagnetiska material kommer bidraget från många atomära moment att ge ett stort makroskopiskt m utan att en yttre ström behöver flyta.

Tillämpningar och exempel

Kompassens nål är ett exempel på en liten stavmagnet vars beteende i jordens magnetfält styrs av dess dipolmoment.
Elektriska motorer och generatorer bygger på vridmomentet mellan strömspolar (med magnetiska moment) och externa magnetfält.
Magnetisk resonans (NMR/MRI) utnyttjar kärnors och elektroners magnetiska dipolmoment i starka fält för att få spektral och bildinformation.

Sammanfattningsvis är det magnetiska dipolmomentet en vektorstorhet som beskriver hur starkt och i vilken riktning ett system interagerar med magnetfält. Det har både klassiska uttryck (ström·area) och kvantmekaniska uttryck (proportionellt mot spinn och orbitalt rörelsemängdsmoment) och spelar en central roll i många fysikaliska fenomen och tekniska tillämpningar.

Två definitioner av moment

I läroböcker används två kompletterande metoder för att definiera magnetiska moment. I läroböcker från före 1930-talet definierades de med hjälp av magnetiska poler. De senaste läroböckerna definierar dem i termer av ampèrianska strömmar.

Definition av magnetisk pol

Fysikerna beskriver källor till magnetiska moment i material som poler. Nord- och sydpolen är en analogi till de positiva och negativa laddningarna i elektrostatik. Tänk på en stavmagnet som har magnetiska poler av samma storlek men motsatt polaritet. Varje pol är en källa till magnetisk kraft som försvagas med avståndet. Eftersom magnetiska poler alltid finns i par upphäver deras krafter delvis varandra, eftersom den ena polen drar, medan den andra stöter bort. Denna upplösning är störst när polerna är nära varandra, dvs. när stavmagneten är kort. Den magnetiska kraft som en stavmagnet ger upphov till i en given punkt i rummet beror därför på två faktorer: dels på polernas styrka p {\displaystyle p} $p$ , dels på vektorn l {\displaystyle \mathbf {l} } som $\mathbf {l}$ skiljer dem åt. Momentet definieras som

m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . } $\mathbf {m} =p\mathbf {l} .$

Den pekar i riktning från södra till norra polen. Analogin med elektriska dipoler bör inte tas för långt eftersom magnetiska dipoler är förknippade med vinkelmoment (se Magnetiskt moment och vinkelmoment). Icke desto mindre är magnetiska poler mycket användbara för magnetostatiska beräkningar, särskilt i tillämpningar på ferromagneter. De som använder sig av den magnetiska polen representerar i allmänhet magnetfältet med det irroterande fältet H {\displaystyle \mathbf {H} } $\mathbf {H}$ i analogi med det elektriska fältet E {\displaystyle \mathbf {E} } $\mathbf {E}$ .

Definition av strömkretsar

Anta att en plan sluten slinga leder en elektrisk ström I {\displaystyle I} och har en vektorarea S {\displaystyle \mathbf {S} } $\mathbf {S}$ ( x {\displaystyle x} , y {\displaystyle y} och z {\displaystyle z} $z$ koordinaterna för denna vektor är areorna av projektioner av slingan på y z {\displaystyle yz} $yz$ , z x {\displaystyle zx} $zx$ och x y {\displaystyle xy} $xy$ ). Dess magnetiska moment m {\displaystyle \mathbf {m} } $\mathbf {m}$ , vektor, definieras som:

m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . } $\mathbf {m} =I\mathbf {S} .$

Enligt konvention anges vektorområdets riktning med hjälp av regeln om högerhandens grepp (högerhandens fingrar krullas i strömriktningen runt slingan, när handflatan "rör" slingans ytterkant, och den raka tummen anger vektorområdets och därmed det magnetiska momentets riktning).

Om slingan inte är plan är momentet givet som följande

m = I2 ∫ r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} . } $\mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} .$

I det mest allmänna fallet med en godtycklig strömfördelning i rymden kan det magnetiska momentet för en sådan fördelning hittas med hjälp av följande ekvation:

m = 12∫ r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}}V,} $\mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,$

där r {\displaystyle \mathbf {r} } $\mathbf {r}$ är positionsvektorn som pekar från ursprunget till volymelementets plats, och J {\displaystyle \mathbf {J} } $\mathbf {J}$ är strömtäthetsvektorn på den platsen.

Ovanstående ekvation kan användas för att beräkna det magnetiska momentet hos en samling rörliga laddningar, t.ex. ett snurrande laddat fast ämne, genom att ersätta

J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,} $\mathbf {J} =\rho \mathbf {v} ,$

där ρ {\displaystyle \rho } $\rho$ är den elektriska laddningstätheten i en given punkt och v {\displaystyle \mathbf {v} } $\mathbf {v}$ är den momentana linjära hastigheten i den punkten.

Exempelvis är det magnetiska momentet som produceras av en elektrisk laddning som rör sig längs en cirkulär bana följande

m = q 12r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}}\,q\,\mathbf {r} \times \mathbf {v} } $\mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v}$ ,

där r {\displaystyle \mathbf {r} } $\mathbf {r}$ är laddningen q {\displaystyle q}s position i förhållande till cirkelns centrum och v {\displaystyle \mathbf {v} } $\mathbf {v}$ är laddningens momentana hastighet.

De som använder sig av modellen med strömkretsar representerar i allmänhet magnetfältet med det solenoida fältet B {\displaystyle \mathbf {B} } $\mathbf {B}$ , analogt med det elektrostatiska fältet D {\displaystyle \mathbf {D} } $\mathbf {D}$ .

Magnetiskt moment hos en solenoid

En generalisering av ovanstående strömslinga är en spole med flera vändningar, eller solenoid. Dess moment är vektorsumman av momenten för de enskilda varven. Om solenoiden har N {\displaystyle N} $N$ identiska varv (enkelskiktslindning),

m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . } $\mathbf {m} =NI\mathbf {S} .$

3D-bild av en solenoid.

Moment m {\displaystyle \mathbf {m} } $\mathbf {m}$ av en plan strömkrets med area S {\displaystyle S} $S$ och ström I {\displaystyle I} .

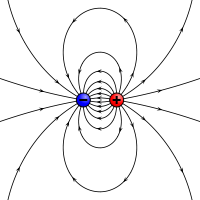
En elektrostatisk motsvarighet till ett magnetiskt moment: två motsatta laddningar som är separerade med ett begränsat avstånd.

Enheter

Enheten för magnetiskt moment är inte en basenhet i det internationella enhetssystemet (SI) och kan representeras på mer än ett sätt. I definitionen av en strömslinga mäts till exempel ytan i kvadratmeter och I {\displaystyle I} mäts i ampere, så det magnetiska momentet mäts i ampere-kvadratmeter ( A m {\displaystyle2 {\text{A m}}^{2}}} ${\text{A m}}^{2}$ ). I ekvationen för vridmoment på ett moment mäts vridmomentet i Newtonmeter och magnetfältet i tesla, så momentet mäts i N.m per Tesla ( N.m T - 1{\displaystyle {\text{N.m T}}^{-1}}} ${\text{N.m T}}^{-1}$ ). Dessa två representationer är likvärdiga:

A m = 2N.m T -1 . {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}. } $\,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}.$

I CGS-systemet finns det flera olika uppsättningar av elektromagnetiska enheter, varav de viktigaste är ESU, Gaussian och EMU. Bland dessa finns det två alternativa (icke likvärdiga) enheter för magnetiskt dipolmoment i CGS:

(ESU CGS) 1 statA-cm² = 3,33564095×10^-14 (m-A² eller N.m/T)

och (mer frekvent använt)

(EMU CGS och Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10^-3 (m-A² eller N.m/T).

Förhållandet mellan dessa två icke-ekvivalenta CGS-enheter (EMU/ESU) är exakt lika med ljusets hastighet i fri rymd, uttryckt i cm/s.

Alla formler i den här artikeln är korrekta i SI-enheter, men i andra enhetssystem kan formlerna behöva ändras. I SI-enheterna har till exempel en strömslinga med strömmen I och ytan A ett magnetiskt moment I×A (se nedan), men i Gaussiska enheter är det magnetiska momentet I×A/c.

Egentliga magnetiska moment och spinn hos vissa elementarpartiklar
Partikel	Magnetiskt dipolmoment i SI-enheter (10 ⁻²⁷J/T).	Spinkvantumtal (dimensionslöst)
Elektron	-9284.764	1/2
proton	14.106067	1/2
neutroner	-9.66236	1/2
muon	-44.904478	1/2
deuteron	4.3307346	1
triton	15.046094	1/2

För förhållandet mellan begreppen magnetiskt moment och magnetisering, se magnetisering.

Frågor och svar

F: Vad är det magnetiska momentet för en magnet?

S: En magnets magnetiska moment är en storhet som bestämmer den kraft som magneten kan utöva på elektriska strömmar och det vridmoment som ett magnetfält kommer att utöva på den.

F: Vilka föremål har magnetiska moment?

S: En elektrisk strömslinga, en stavmagnet, en elektron, en molekyl och en planet har alla magnetiska moment.

F: Hur kan man ta hänsyn till både det magnetiska momentet och magnetfältet?

S: Både det magnetiska momentet och magnetfältet kan betraktas som vektorer med en storlek och riktning.

F: I vilken riktning pekar det magnetiska momentet i en magnet?

S: Det magnetiska momentets riktning pekar från syd- till nordpolen på en magnet.

F: Vad är förhållandet mellan det magnetiska momentet och magnetfältet hos en magnet?

S: Det magnetfält som alstras av en magnet är proportionellt mot dess magnetiska moment.

F: Vad avses normalt med termen magnetiskt moment?

S: Mer exakt avser termen magnetiskt moment normalt ett systems magnetiska dipolmoment, som ger den första termen i multipolexpansionen av ett allmänt magnetfält.

F: Hur beter sig dipolkomponenten i ett objekts magnetfält när avståndet från objektet ökar?

S: Dipolkomponenten i ett objekts magnetfält är symmetrisk kring riktningen för dess magnetiska dipolmoment, och minskar som den omvända kuben av avståndet från objektet.

Sök