Osäkerhetsprincipen | även kallad Heisenbergs osäkerhetsprincip

Diagram

 
6. Den här animationen visar en av de viktiga konsekvenserna av universums osäkerhetskaraktär: kvanttunnling av elektroner. Titta noga. Varje gång kommer en liten bit igenom barriären.  


5. Genom att hänga upp mittgapet med fjäderskalor kan man mäta rörelsemängden, men detta gör att gapet flyttas på ett oförutsägbart sätt så att informationen om var varje foton befinner sig i mitten går förlorad.  


4. En fjäder som monterar en barriär med ett litet hål gör att partikeln klämmer sig igenom hålet, vilket trycker på barriären, sträcker ut fjädrarna och mäter på så sätt rörelsemängden. Men eftersom den fjädermonterade barriären rör sig är vi mindre säkra på var partikeln befann sig när den gick genom hålet, och diffraktion kommer också att påverka dess position på detektionsskärmen.  


3. När hålet blir smalare ökar säkerheten för var fotonen befinner sig i mitten, men dess riktning därifrån till detektionsskärmen till höger blir motsvarande osäkrare. Fokuseringen blir suddig. Om man vidgar hålet gör man att alla fotonerna hamnar i mitten av detektionsskärmen, men då har vi mindre säker uppfattning om var de befann sig när de gick genom den centrala barriären.  


2. När hålet smalnar av kröker partiklarna sina banor runt hålets kanter (diffraktion) så att den resulterande strålen blir större och mjukare.  


1. Fotoner, elektroner och andra subatomära partiklar kommer att bli skarpt fokuserade när de skjuts genom ett stort hål, men vi vet inte exakt var de befann sig i mitten av vägen.  

Hur lärde sig människan om osäkerhet?

Mycket kort efter att Werner Heisenberg skapade den nya kvantfysiken kom något oväntat direkt från hans matematik, nämligen uttrycket:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad \qquad }

Felområdet för positionen (x) gånger felområdet för rörelsen (p) är ungefär lika med eller större än Planckkonstanten dividerad med 4π.

Dessa symboler uttrycker i matematisk form det som du redan har sett i bilderna ovan. Symbolerna säger på ett tydligt sätt att man inte kan vara helt säker på var något är och vart det är på väg. Om du får en tydligare uppfattning om var det befinner sig vid en viss tidpunkt har du en mindre säker uppfattning om vart det är på väg och hur snabbt det är på väg. Om man blir klarare över var den är på väg och hur snabbt den är vid något tillfälle, har man mindre uppfattning om var den är just nu.

Forskarna hade redan lärt sig varför vissa ämnen avger karakteristiska ljusfärger när de upphettas eller på annat sätt exciteras. Heisenberg försökte förklara varför dessa färger har en karakteristisk ljusstyrka. Det hade inte räckt om han och de andra vetenskapsmännen bara hade sagt: "Ja, det är så det är". De var säkra på att det måste finnas en god anledning till dessa skillnader och till det faktum att förhållandet mellan de ljusa linjernas styrka alltid var detsamma för varje prov av ett grundämne.

Han hade ingen aning om att han skulle snubbla över en dold naturhemlighet när han gav sig iväg för att hitta förklaringen till intensiteten i de färgade linjerna som är karakteristiska för varje grundämne. Studiet av kvantmekaniken hade redan visat varför väte har fyra ljusa linjer i den del av spektrumet som människor kan se. Det måste ha verkat som om nästa sak att lära sig skulle vara hur man beräknar deras ljusstyrka. Vätgas verkade vara det självklara stället att börja på eftersom väte bara har en elektron att hantera och bara fyra linjer i den synliga delen av spektrumet. Det måste väl finnas en bra anledning till att de inte är lika ljusstarka. Förklaringen till ljusstyrkan hos de olika färgade linjerna hos neon och de andra grundämnena kunde vänta.

Heisenberg började arbeta med kvantfysik genom att anpassa de klassiska ekvationerna för elektricitet, som till att börja med är mycket komplicerade, så matematiken bakom hans artikel från 1925 var mycket svår att följa.

Han försökte hitta det rätta sättet att beräkna intensiteten hos ljusa linjer i vätgaslampans spektrum. Han var tvungen att hitta en relaterad storhet som kallas "amplitud" och multiplicera amplitud med amplitud (eller med andra ord kvadrera amplituden) för att få den intensitet han ville ha. Han var tvungen att ta reda på hur han skulle uttrycka amplituden på ett sätt som tog hänsyn till det faktum att vätgaslampor inte utstrålar vid alla frekvenser och inte utstrålar över ett kontinuerligt frekvensområde i den del av spektrumet som människor kan se. Heisenberg hittade ett anmärkningsvärt nytt sätt att beräkna amplitud.

Den märkliga ekvation som Heisenberg upptäckte och använde för att multiplicera en kvantmängd (t.ex. position) med en annan (t.ex. rörelse) publicerades i vad som har kallats "Heisenbergs 'magiska' papper från juli 1925".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\}\,A(n,n-a)B(n-a,n-b)}

Matematiken ovan ser väldigt svår ut, men den matematik som föregår den är mycket svårare och är extremt svår att förstå. Den ges här bara för att visa hur den såg ut. Heisenbergs uppsats är en historisk milstolpe. Många av de fysiker som läste hans uppsats sade att de inte kunde säga emot hans slutsatser, men att de inte kunde följa hans förklaring av hur han kom fram till dessa slutsatser. De begynnelsekvationer som Heisenberg använde sig av involverade Fourierserier, och involverade många faktorer. Vi kommer att återkomma till ekvationen ovan eftersom den är ett slags recept för att skriva ut och multiplicera matriser.

De nya ekvationerna var tvungna att vara så märkliga och ovanliga eftersom Heisenberg beskrev en märklig värld där vissa saker, t.ex. elektronernas banor, inte långsamt blir större eller mindre. De nya typerna av förändringar innebär hopp och stora luckor mellan hoppen. Elektroner kan bara hoppa mellan vissa banor, och den energi som vinns eller förloras vid bytet mellan banorna produceras när en foton med rätt energi absorberas eller en ny foton med rätt energi produceras. Om elektroner i väteatomer oftast hoppar ner (faller) mellan två särskilda banor, kommer fler fotoner att avges på den energinivån, och därför kommer det ljus som produceras på den nivån att vara mest intensivt.

Det var svårt att få ekvationer som är byggda för kontinuerliga spektrum (det du ser när du skickar solens ljus genom ett prisma) att passa till spektrum som bara har några få toppfrekvenser mellan vilka det inte finns något. Nästan allt som man redan hade lärt sig om ljus och energi hade gjorts med stora föremål som brinnande ljus eller solar, och dessa stora föremål producerar alla kontinuerliga spektrum. Även om dessa vanliga stora saker var lätta att göra experiment med hade det ändå tagit lång tid att ta reda på de lag(fysik)lagar som styr dem. Nu hade fysikerna att göra med saker som var för små för att kunna ses, saker som inte producerade kontinuerliga spektrum, och de försökte hitta ett sätt att åtminstone få ledtrådar från det de redan visste som skulle hjälpa dem att hitta lagarna för dessa små och glesa ljuskällor.

De ursprungliga ekvationerna handlade om ett slags vibrerande kropp som skulle producera en våg, lite på samma sätt som ett rörblad i en orgel skulle producera en ljudvåg med en karakteristisk frekvens. Det fanns alltså en rörelse fram och tillbaka (som rörelsens vibrationer) och det fanns en utsänd våg som kunde ritas som en sinusvåg. Mycket av det man tidigare hade kommit fram till om fysik på atomnivå hade att göra med elektroner som rörde sig runt atomkärnor. När en massa rör sig i en omloppsbana, när den roterar runt något slags nav, har den vad som kallas "vinkelmoment". Vinkelmoment är det sätt på vilket något som en karusell fortsätter att rotera efter att folk har slutat att skjuta på den. Den matematik som används för fasberäkningar och vinkelmoment är komplicerad. Dessutom visade Heisenberg inte alla sina beräkningar i sin artikel från 1925, så även duktiga matematiker kan ha svårt att fylla i det han inte sa.

Även om många fysiker säger att de inte kan räkna ut de olika matematiska stegen i Heisenbergs genombrottsartikel, använder en färsk artikel som försöker förklara hur Heisenberg kom fram till sitt resultat tjugo sidor fyllda av matematik. Inte ens den artikeln är lätt att förstå. Matematiken började med en del riktigt svåra saker och skulle till slut leda till något relativt enkelt som visas högst upp i den här artikeln. Det var inte lätt att få fram det enklare resultatet, och vi ska inte försöka visa hur man går från en föråldrad bild av universum till den nya kvantfysiken. Vi behöver bara tillräckligt med detaljer för att visa att nästan så snart Heisenberg gjorde sitt genombrott kom en del av hur universum fungerar som ingen hade sett tidigare i blickfånget.

Heisenberg måste ha varit mycket upphetsad men också mycket trött när han sent på kvällen äntligen fick sitt genombrott och började bevisa för sig själv att det skulle fungera. Nästan genast märkte han något märkligt, något som han trodde var ett irriterande litet problem som han på något sätt kunde få bort. Men det visade sig att detta lilla besvär var en stor upptäckt.

Heisenberg hade arbetat för att multiplicera amplituder med amplituder, och nu hade Heisenberg ett bra sätt att uttrycka amplitud med hjälp av sin nya ekvation. Naturligtvis tänkte han på multiplikation, och på hur han skulle multiplicera saker som gavs i termer av komplicerade ekvationer.

Heisenberg insåg att han förutom att kvadrera amplituden så småningom skulle vilja multiplicera positionen med rörelsen eller multiplicera energin med tiden, och det såg ut som om det skulle göra skillnad om han vände på ordningen i dessa nya fall. Heisenberg tyckte inte att det skulle spela någon roll om man multiplicerade position med impuls eller om man multiplicerade impuls med position. Om de bara hade varit enkla tal skulle det inte ha varit något problem. Men de var båda komplicerade ekvationer, och hur man fick fram siffrorna som skulle sättas in i ekvationerna visade sig vara olika beroende på vilket sätt man började. I naturen var man tvungen att mäta positionen och sedan mäta drivkraften, eller så var man tvungen att mäta drivkraften och sedan mäta positionen, och i matematiken rådde samma allmänna situation. (Se den engelska Wikipediaartikeln Heisenbergs ingång till matrismekaniken om du vill lära dig de krångliga detaljerna!). De små men irriterande skillnaderna mellan resultaten skulle finnas kvar, hur mycket Heisenberg än önskade att de skulle försvinna.

Heisenberg kunde då inte bli av med detta lilla problem, men han var utmattad, så han lämnade in sitt arbete till sin närmaste chef, Max Born, och gick på semester.

Max Born var en anmärkningsvärd matematiker som snart insåg att ekvationen som Heisenberg hade gett honom var ett slags recept för att skriva en matris. Dr Born var en av de få personer som vid den här tiden var intresserade av denna märkliga typ av matematik som de flesta trodde inte var användbar till särskilt mycket. Han visste att matriser kunde multipliceras, så att göra alla beräkningar för att redovisa ett fysikproblem kunde hanteras genom att multiplicera en matris med en annan. Bara att kunna sätta ett komplicerat förfarande i en standardiserad och godtagbar form skulle göra det lättare att arbeta med. Det skulle också kunna göra det lättare för andra människor att acceptera det.

Born var en så duktig matematiker att han nästan omedelbart insåg att om man bytte ordning för att multiplicera de två matriserna skulle man få ett annat resultat, och att resultaten skulle skilja sig åt med en liten mängd. Denna mängd skulle vara h/2πi. I vardagen skulle denna skillnad vara så liten att vi inte ens skulle kunna se den.

 
Två vågor som inte är i fas med varandra.  


Solens hela visuella spektrum. Det finns inga luckor. Detta diagram visar intensiteten vid de olika frekvenserna.  


Neonspektrum  


Spektrum av väte  


När vissa molekyler exciteras ger de ifrån sig en karakteristisk färg.  

Till en formell teori om osäkerhet

Det tog några år, men Heisenberg kunde bevisa osäkerhetsprincipen, som säger att Δx × Δp = h/2, vilket är det tal som kommer ut ur de ursprungliga ekvationerna, men som utelämnar π och i som har att göra med fasförändringar. Heisenberg förklarade att han härledde sin osäkerhetsprincip från detta tidigare resultat när han 1927 skrev en artikel där han introducerade denna teori.

Konstanten h, som kallas Planckkonstanten, är en mystisk siffra som ofta förekommer, så vi måste förstå vad denna lilla siffra är. Numeriskt brukar det anges som 6,62607×10^-34 J s (joule sekunder). Det är alltså en storhet som involverar energi och tid.

Den upptäcktes när Planck insåg att energin från en perfekt strålare (en så kallad svartkroppsstrålare) avges i enheter av bestämd storlek som kallas "kvanta" (singular av detta ord är "kvantum"). Den utstrålade energin avges som fotoner, och frekvensen hos en foton är proportionell mot den "slagkraft" den ger. Vi upplever olika frekvenser av synligt ljus som olika färger. I den violetta änden av spektrumet har varje foton en relativt stor mängd energi; i den röda änden av spektrumet har varje foton en relativt liten mängd energi. Sättet att beräkna energimängden hos en foton ges av ekvationen E = hν (energi är lika med Planckkonstanten gånger "nu" eller frekvens).

Heisenbergs osäkerhetsprincip Δx × Δp ≥ h säger oss att när vi försöker fastställa vissa talpar kan vi bara komma så nära, och att om vi försöker bli tydligare med ett av dem, dvs. om vi försöker göra Δx mindre så att vi får en bättre uppfattning om var något befinner sig, måste vi få tillbaka ett större tal för det andra talet i paret, och att det belopp som skiljer de två talen åt är nära relaterat till h.

Ett annat par fysiska storheter följer osäkerhetsförhållandet: ΔE × Δt ≥ h, och det paret visar bland annat att om vi letar i den interstellära rymden, på en plats där vi inte förväntar oss att hitta något alls, och vi minskar Δt närmare och närmare 0, så måste ΔE bli större och större för att behålla balansen som visas i ekvationen - och plötsligt kan något med dynamik dyka upp bara för den korta tidsperioden.

Hur förklaras denna obestämdhet (brist på säkerhet)? Vad händer i universum? Det sägs ofta att en ny teori som är framgångsrik kan ge ny information om de fenomen som undersöks. Heisenberg skapade en matematisk modell som förutspådde de korrekta intensiteterna för vätgasens ljusa linjespektrum, men utan att ha för avsikt att göra det upptäckte han att vissa par av fysiska storheter avslöjar en oväntad osäkerhet. Fram till dess hade ingen haft en aning om att mätningar inte i all evighet kunde göras mer och mer exakta och exakta. Det faktum att de inte kunde göras säkrare, mer definitiva, var en fantastisk ny upptäckt. Många människor var inte villiga att acceptera det.

Bohr och hans kollegor hävdade att fotoner, elektroner etc. inte har någon position eller rörelse förrän de mäts. Denna teoretiska ståndpunkt växte fram ur upptäckten av osäkerheten och var inte bara en personlig preferens om vad man skulle tro. Bohr menade att vi inte vet något om något som en foton eller elektron förrän vi observerar den. För att kunna observera en sådan liten sak måste vi interagera med den på något sätt. I vardagslivet är det möjligt att göra något som att gå bredvid en bil och samtidigt anteckna de gånger den passerar punkter på ett rutnät som ritats in på trottoaren. Kanske kommer bilens egen vikt att trycka ner små spakar i trottoaren som slår ut klockor som är fästade vid var och en av dem och registrerar bilens vikt. I slutändan skulle vi ha ett tydligt register över var bilen befann sig vid olika tidpunkter, och vi skulle också kunna beräkna bilens färdriktning och vikt. Vi skulle då vid varje tidpunkt på klockan kunna veta både dess position och dess rörelse (dess hastighet multiplicerad med dess massa). Vi skulle inte ens föreställa oss att den kraft som krävs för att flytta de små spakarna skulle ha någon inverkan på bilens framfart. Vi skulle inte heller föreställa oss att bilen inte hade någon position eller bana mellan de punkter på trottoaren där det finns spakar, eller att bilen existerar i ett slags tredimensionell oskärpa under dessa tider och bara slår sig ner när den trycker ner en spak. Den värld som vi är bekanta med avslöjar inte dessa märkliga typer av interaktioner.

För att lokalisera ett fartyg på havet under den mörkaste natten kan vi använda en sökarlampa, och det ljuset skulle inte störa fartygets position eller färdriktning, men för att lokalisera en elektron med hjälp av ljus skulle det krävas att den träffas av en eller flera fotoner som var och en har tillräckligt med rörelsekraft för att störa elektronens position och färdriktning. Att lokalisera elektronen med andra medel skulle innebära att man måste hålla den i någon form av fysisk begränsning som också skulle avbryta dess rörelse framåt.

För att lokalisera en foton är det bästa man kan göra utan att avbryta dess rörelse framåt att få den att gå genom ett cirkulärt hål i en barriär. Om man vet när fotonen sändes ut (t.ex. av en laser) och när fotonen anländer till en detektionsskärm, t.ex. en digitalkamera, kan man beräkna den tid som krävs för att färdas denna sträcka och den tid som fotonen passerade genom hålet. För att fotonen ska kunna passera måste det cirkulära hålet dock ha en diameter som är större än fotonens storlek. Ju mindre det cirkulära hålet är, desto närmare kommer vi att veta den exakta positionen för fotonen när den passerar genom det. Vi kan dock aldrig veta om fotonen är ocentrisk vid den tidpunkten. Om hålet är exakt lika stort som fotonen kommer den inte att passera igenom. När hålets diameter minskas förändras momentumet eller riktningen för fotonen när den lämnar hålet mer och mer kraftigt.

Niels Bohr och hans kollegor hävdade att vi får stora problem om vi antar att det som är för litet för att kunna ses ens i ett mikroskop är sant, något som vi har bevis för endast på vardagslivets skala. I vardagslivet har saker och ting alltid en bestämd position. På atomnivå har vi inga bevis för att stödja denna slutsats. I vardagslivet har saker och ting en bestämd tidpunkt då de inträffar. På den atomära skalan har vi inga bevis för att stödja denna slutsats. Om man i vardagslivet observerar en fabrik från nattskiftet dag ett till dagskiftet dag två och ser en färdig bil rullas ut till lastkajen, skulle det inte vara meningsfullt att säga att det är omöjligt att säga om den levererades under nattskiftet eller under dagskiftet. Men på atomnivå kan vi visa exempel på fall då vi måste räkna en enda foton som producerad vid två tillfällen. (Om det inte är tillräckligt illa kan vi också visa fall där en enda foton produceras av två intilliggande lasrar).

En del av svårigheten med att ta reda på vad som händer på atomär nivå är att vi vill veta både var något är och vad dess bana är, och veta båda sakerna samtidigt, men vi kan inte mäta både position och bana samtidigt. Antingen mäter vi en fotons eller elektronens rörelse vid ett tillfälle och mäter sedan utan större fördröjning än nödvändigt dess position, eller så byter vi om och mäter positionen först och rörelse sedan. Problemet är att vi genom att få den första att anta en ganska bestämd form (genom att pressa ner den på något sätt) ökar vi osäkerheten som är involverad i nästa mätning. Om våra första mätningar var så grova att många fel infördes i var och en av dem, skulle vi kunna förbättra saker och ting genom att använda ett lättare grepp för att göra var och en av dem, men vi skulle aldrig kunna komma över en viss gräns för noggrannhet.

Vi vet från vardagslivet att om man försöker väga något på en badrumsvåg som placeras på en tvättmaskin som är i centrifugering, kommer resultatet att bli felaktigt eftersom nålen på vågen kommer att röra sig kraftigt. Vi kan stänga av tvättmaskinen. Men för mycket exakta mätningar upptäcker vi att lastbilar som kör förbi i grannskapet får nålen att röra sig, så vi kan ställa vågen på något som isolerar den från störningar utifrån. Vi tror att vi kan eliminera vibrationerna tillräckligt mycket för att ge oss resultat som är precis så exakta som vi vill ha. Vi tänker aldrig på att det som står på vågen i sig själv vibrerar eller att det har en obestämd dynamik.

Om man argumenterar bakåt från osäkerhetsprincipen ser det ut som om det i själva verket inte finns någon bestämd position och ingen bestämd rörelse för något ting på atomär skala, och att experimenterare bara kan tvinga saker och ting till bestämdhet inom den gräns som anges i osäkerhetsprincipen. Bohr och hans kollegor hävdade bara att vi inte kunde veta någonting utan att göra mätningar, och när mätningar görs kan vi tvinga saker och ting i riktning mot en mer bestämd position eller ett mer bestämt momentum, men att vi inte kan få den absoluta bestämdhet eller säkerhet som vi skulle vilja ha. Men andra tog möjligheten på allvar och hävdade att om matematiken stämmer så kan det inte finnas någon bestämdhet eller säkerhet i den ultra lilla världen. Vetenskapens natur är att matematiken bara är en modell av verkligheten, och det finns ingen garanti för att det är en korrekt modell.

Matematiken och de praktiska konsekvenserna av de saker som matematiken förutsäger är så tillförlitliga att det är mycket svårt att säga emot dem, men vad matematiken säger om den verkliga världen har gett upphov till flera olika idéer. Bland de vetenskapsmän som arbetade med Niels Bohr i Köpenhamn ansåg man att osäkerhetsprincipen innebar att det fysiska universum på en elementär nivå inte existerar i en deterministisk form. Det är snarare en samling sannolikheter eller potentialer.

I motsats till Köpenhamnsgruppens berättelse som vävs runt matematiken finns det andra berättelser, t.ex. "multipla universumtolkningen" som säger att varje gång det finns flera möjliga utfall enligt kvantteorin, uppstår varje utfall i ett eget nytt universum. Einstein hävdade att det inte finns flera möjliga utfall, så det finns bara ett universum och det är bestämt, eller, som han uttryckte det, "Gud spelar inte tärning".

 
Om h var den minsta möjliga energimängden skulle den grundläggande ekvationen som visar energin i fotoner av olika frekvens inte vara i balans. Den skulle vara felaktig.  

Invändningar mot osäkerhetsprincipen

Albert Einstein såg att den nya kvantmekaniken innebar att det saknades position och momentum i tiden innan mätningarna gjordes, och han protesterade kraftigt. Han var övertygad om att saker och ting hade bestämda positioner och bestämda impulser innan de mättes, och att det faktum att mätning av en av ett par saker och stör möjligheten att noggrant mäta den andra inte talar för att det saknas någon av dem i förväg. Han och två av hans kolleger skrev det som har kommit att kallas "EPR-papperet". Där hävdas att det måste finnas egenskaper som bestämmer position och rörelse och att om vi kan se dem, eller om vi kan få information om dem, kan vi matematiskt känna till och förutsäga position och rörelse. Länge trodde man att det inte fanns något sätt att bevisa eller motbevisa det som för Einstein var en trosartikel. Argumentet var mycket produktivt eftersom det ledde till all den moderna utvecklingen inom intrikation.

Matematiskt sett har Einstein bevisats ha fel. År 1964 utvecklade John Stewart Bell en matematisk metod för att skilja mellan beteendet hos två partiklar som har bestämda tillstånd som bara är okända för de två individer som undersöker dem, och två partiklar som har sammanflätade tillstånd som är obestämda eller osäkra tills de mäts. Hans metod visar att sannolikheten för att få vissa resultat är olika under de två olika antagandena. Hans arbete kallas Bells sats eller Bells ojämlikhet. Experiment har visat att naturen beter sig så som Bell beskriver den.

 

En annan väg till osäkerhet

De första diskussionerna om Heisenbergs osäkerhetsprincip byggde på en modell som inte tog hänsyn till att materiepartiklar som elektroner, protoner etc. har en våglängd. År 1926 visade Louis de Broglie att alla ting, inte bara fotoner, har en egen frekvens. Saker och ting har en vågnatur och en partikelnatur, precis som fotoner. Om vi försöker göra vågen för en sak som en proton smalare och högre skulle det göra dess position tydligare, men då skulle rörelsen bli mindre väldefinierad. Om vi försöker göra impulsdelen av en vågbeskrivning tydligare, dvs. få den att hålla sig inom ett smalare värdeintervall, så sprider sig vågtoppen och dess position blir mindre bestämd.

Den våg som ingår i beskrivningen av en foton är enligt kvantmekaniken inte samma sak som en våg på havsytan eller de områden av komprimerad luft och förtunnad luft som utgör ljudvågor. I stället har dessa vågor toppar eller områden med hög amplitud som har att göra med sannolikheten att hitta något vid den punkten i tid och rum. Mer exakt är det kvadraten på amplituden som ger sannolikheten för att något fenomen ska dyka upp.

Den våg som gäller för en foton kan vara en ren sinusvåg. I det fallet skulle kvadraten på värdet av varje topp ge sannolikheten att observera fotonen i den punkten. Eftersom amplituderna hos sinusvågorna är lika stora överallt, skulle sannolikheten för att hitta fotonen vid var och en av dem vara densamma. Så i praktiken skulle det inte ge någon ledtråd om var man kan leta efter en av dessa fotoner om man känner till vågen för en av dessa fotoner. Å andra sidan är en fotons rörelsemängd matematiskt relaterad till amplituden av dess våg. Eftersom vi i det här fallet har en ren sinusvåg är amplituden för varje cykel av vågen densamma och därför finns det bara ett momentumvärde förknippat med denna våg. Vi skulle inte veta var fotonen skulle träffa, men vi skulle veta exakt hur hårt den skulle träffa.

I ljusstrålar som fokuserar på en punkt på en detektionsskärm är de vågor som är kopplade till fotonerna inte rena sinusvågor. I stället är det vågor med hög amplitud vid en punkt och mycket lägre amplituder på vardera sidan om den högsta toppen. Matematiskt är det möjligt att analysera en sådan våg i ett antal olika sinusvågor med olika våglängder. Det är lite lättare att visualisera den omvända processen genom att titta på en inledande sinusvåg med en frekvens till vilken läggs en andra sinusvåg med en annan våglängd, sedan en tredje, sedan en fjärde och så vidare. Resultatet blir en komplex våg som visar en hög topp och som innehåller ett stort antal vågor med olika våglängder och därmed olika momentum. I det fallet är sannolikheten att fotonen kommer att dyka upp vid en viss punkt extremt hög, men det momentum som den levererar kan visa sig vara relaterat till våglängden hos någon av de ingående vågorna. Med andra ord är värdet p = ħ/λ inte längre ett enda värde eftersom alla längder på de sammansatta "vågorna med olika våglängd" måste beaktas.

Simuleringen visar hur man matematiskt kan modellera skärpningen av en partikels position: Överlagra många olika vågformer över den ursprungliga sinusvågen. Centret kommer att bilda en högre och högre topp, och resten av topparna kommer att öka i antal men minska i höjd eftersom de kommer att interferera med varandra. Så i slutändan finns det många olika vågor i superpositionen, var och en med en annan våglängd och (genom p = ħ/λ) ett annat momentum, men bara en mycket hög topp, en topp som blir högre och smalare och ger oss något som ligger närmare och närmare en bestämd position.

För att göra momentumet mer och mer definitivt måste vi ta bort mer och mer av de överlagrade sinusvågorna tills vi bara har en enkel sinusvåg kvar. På så sätt skulle vi gradvis minska höjden på den centrala toppen och gradvis öka höjderna på de konkurrerande platserna där man skulle kunna hitta partikeln.

Så när vi börjar med en vågbild av subatomära partiklar kommer vi vanligtvis alltid att ha att göra med fall med relativt höga centrala toppar och relativt många komponentvåglängder. Det kommer aldrig att finnas en exakt position eller ett exakt momentum som kan förutsägas under dessa omständigheter. Om den matematiska modellen är en korrekt återgivning av den verkliga världen har ingen foton eller annan subatomär partikel vare sig en exakt position eller ett bestämt momentum. När vi mäter en sådan partikel kan vi välja en metod som ytterligare pressar ihop toppen och gör den smalare, eller så kan vi välja en metod som sänker toppen och jämnar ut de ingående våglängderna. Beroende på vad vi mäter och hur vi mäter det kan vi få vår position att bli mer bestämd eller vi kan göra vårt impulsområde smalare. Vi kan vara försiktiga när vi utformar experimentet för att undvika olika sätt att manipulera apparaten, men vi kan inte bli av med det faktum att det inte fanns något helt säkert från början.

 
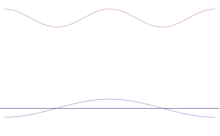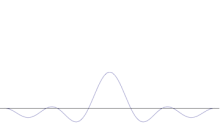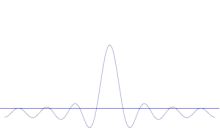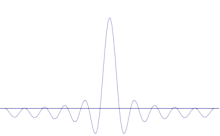
Överlagring av flera plana vågor. Vågpaketet blir alltmer lokaliserat när många vågor läggs till. Fouriertransformen är en matematisk operation som separerar ett vågpaket i dess enskilda plana vågor. Observera att de vågor som visas här endast är reella i illustrativt syfte, medan vågfunktionen i kvantmekaniken i allmänhet är komplex.  

Kulturella influenser

Heisenbergs osäkerhetsprincip har i hög grad påverkat argumenten om fri vilja. Enligt den klassiska fysikens teorier är det möjligt att hävda att lagarna om orsak och verkan är obevekliga och att när universum väl har börjat på ett visst sätt kan alla materiens och energins interaktioner som kommer att ske i framtiden beräknas utifrån detta utgångsläge. Eftersom allting absolut är resultatet av det som föregick det, hävdade de, var varje beslut som en människa fattar och varje situation som denna människa hamnar i förutbestämd sedan tidernas begynnelse. Vi har alltså inget val i vad vi gör.

Människor som tror på den fria viljan hävdar att kvantmekanikens lagar inte förutsäger vad som kommer att hända, utan bara vad som är mer eller mindre sannolikt att hända. Därför är varje handling resultatet av en serie slumpmässiga "myntkast" och inget beslut kan spåras tillbaka till en uppsättning nödvändiga förutsättningar.

Uttrycken "kvantsprång" och "kvanthopp" har blivit vanliga sätt att tala om saker och ting. Vanligtvis vill man beskriva något som en enorm förändring som sker under en kort tidsperiod. Uttrycket gäller egentligen det sätt på vilket en elektron beter sig i en atom, antingen när den absorberar en foton som kommer in utifrån och därmed hoppar från en bana runt atomkärnan till en högre bana, eller när den avger en foton och därmed faller från en högre bana till en lägre bana. Niels Bohrs och hans kollegers idé var att elektronen inte rör sig mellan banor utan istället försvinner den från en bana och dyker omedelbart upp i en annan bana. Ett kvanthopp är alltså egentligen inte någon världsomvälvande förändring, utan en plötslig liten förändring.

När människor mäter en process på subatomär nivå och osäkerhetsprincipen visar sig, kan man säga att mänsklig verksamhet har påverkat det som mäts. Om man gör en mätning för att få en säker indikation på en partikels position kommer detta oundvikligen att påverka dess rörelseförmåga, och oavsett vad som görs för att mäta denna rörelseförmåga så snart som möjligt efter det att positionen har mätts, kan sannolikheten för vilken rörelseförmåga som kommer att upptäckas inte undgå att ha ändrats. Osäkerhetsprincipen kan alltså förklara vissa typer av störningar som produceras av undersökare som påverkar resultaten av ett experiment eller en observation. Alla observatörseffekter beror dock inte på kvanteffekter eller på osäkerhetsprincipen. Resten är "observatörseffekter" men inte kvantosäkerhetseffekter.

Observatörseffekter omfattar alla slags saker som verkar på vår vanliga mänskliga skala av händelser. Om en antropolog försöker få en klar uppfattning om livet i ett primitivt samhälle, men hans eller hennes närvaro upprör det samhälle han eller hon besöker, kan de observationer som görs bli mycket missvisande. Ingen av de relevanta interaktionerna sker dock på den nivå som beskrivs av kvantmekaniken eller osäkerhetsprincipen.

Ibland används ordet "quantum" i reklamsyfte för att beteckna något nytt och kraftfullt. Tillverkaren av små bensinmotorer, Briggs and Stratton, har till exempel en serie fyrcylindriga motorer med låga hästkrafter för bensingräsklippare och liknande trädgårdsredskap som de kallar "Quantum".

 

Mer läsning

• Introduktion till kvantteorin, s. 115 och s. 158.

J.P. McEvoy och Oscar Zarate