Heisenbergs osäkerhetsprincip | de viktigaste resultaten av 1900-talets fysik

Förvirring med observatörseffekt

Historiskt sett har osäkerhetsprincipen förväxlats med en liknande effekt inom fysiken, som kallas observatörseffekten. Denna säger att mätningar av vissa system inte kan göras utan att systemen påverkas. Heisenberg erbjöd en sådan observatörseffekt på kvantnivå som en fysisk "förklaring" till kvantosäkerheten.

Det är dock nu uppenbart att osäkerhetsprincipen är en egenskap hos alla vågliknande system. Den uppstår i kvantmekaniken helt enkelt på grund av alla kvantobjekts materiella vågkaraktär. Osäkerhetsprincipen anger alltså faktiskt en grundläggande egenskap hos kvantsystem, och är inte ett uttalande om den nuvarande teknikens observationsframgång. "Mätning" innebär inte bara en process där en fysikobservatör deltar, utan snarare varje interaktion mellan klassiska och kvantobjekt oavsett observatör.

 

Idén om obestämdhet

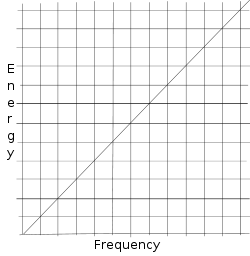
Osäkerhetsprincipen kommer från Werner Heisenbergs matrismekanik. Max Planck visste redan att energin i en ljusenhet är proportionell mot frekvensen för denna ljusenhet ( E ∝ ν {\displaystyle E\propto \nu } ), och att energimängden kan uttryckas i välkända termer som joule med hjälp av en proportionalitetskonstant. Den konstant han gav världen kallas nu Planckkonstanten och representeras av bokstaven h. När matriser används för att uttrycka kvantmekanik måste ofta två matriser multipliceras för att få fram en tredje matris som ger det svar som fysikern försöker hitta. Men om man multiplicerar en matris som P (för rörelsemängd) med en matris som X (för position) får man en annan svarsmatris än den man får när man multiplicerar X med P. Resultatet av att multiplicera P med X och X med P och sedan jämföra dem innehåller alltid Planckkonstanten som en faktor. Det tal som används för att skriva Planckkonstanten kommer alltid att bero på det använda mätsystemet. (Med ett visst mätsystem är dess numeriska värde ett.) Lutningen på linjen i diagrammet till höger som visar förhållandet mellan frekvens och energi kommer också att bero på det valda mätsystemet.

Följande diagram visar vad som händer när vi försöker mäta både plats och momentum.

Det praktiska resultatet av denna matematiska upptäckt är att när en fysiker gör positionen tydligare blir drivkraften mindre tydlig, och när fysikern gör drivkraften tydligare blir positionen mindre tydlig. Heisenberg sade att saker och ting är "obestämda", och andra människor tyckte om att säga att de var "osäkra". Men matematiken visar att det är sakerna i världen som är obestämda eller "luddiga", och inte att det bara är människor som är osäkra på vad som händer.

 
Genom att hänga upp mittspalten med fjädrar kan man mäta rörelsemängden, men spalten förflyttas oförutsägbart så att informationen om fotonens position i mitten går förlorad.  


Det fjädermonterade hålet mäter momentum  


Smalt hål, diffust fokus  


Om gapet minskar ökar säkerheten för var fotonen befinner sig i mitten, men dess riktning därifrån till detektionsskärmen till höger blir motsvarande osäkrare.  


Stort hål, skarpt fokus  



 

Att sätta obestämdhet i matematisk form

Här ska vi visa den första ekvationen som gav den grundläggande idén som senare kom till uttryck i Heisenbergs osäkerhetsprincip.

I Heisenbergs banbrytande artikel från 1925 används och nämns inte ens matriser. Heisenbergs stora framgång var det "system som i princip kunde bestämma de relevanta fysiska egenskaperna (övergångsfrekvenser och amplituder) på ett unikt sätt" för vätestrålning.

Efter att Heisenberg hade skrivit sin genombrottsartikel gav han den till en av sina lärare för att fixa till den och åkte sedan på semester. Max Born blev förbryllad av ekvationerna och de icke-kommuterande ekvationerna som även Heisenberg tyckte var ett problem. Efter flera dagar insåg Born att dessa ekvationer var anvisningar för att skriva ut matriser. Matriser var nya och konstiga, även för dåtidens matematiker, men hur man räknar med dem var redan klart känt. Han och några andra arbetade ut allt i matrisform innan Heisenberg kom tillbaka från sin ledighet, och inom några månader gav den nya kvantmekaniken i matrisform dem underlag för en annan uppsats.

Max Born såg att när matriserna som representerar pq och qp beräknades skulle de inte vara lika. Heisenberg hade redan sett samma sak i sitt ursprungliga sätt att skriva ut saker och ting, och Heisenberg kan ha gissat vad som nästan omedelbart var uppenbart för Born - att skillnaden mellan svarsmatriserna för pq och qp alltid skulle involvera två faktorer som kom från Heisenbergs ursprungliga matematik: Plancks konstant h och i, som är kvadratroten av negativ ett. Så själva idén om det som Heisenberg föredrog att kalla "obestämdhetsprincipen" (vanligtvis känd som osäkerhetsprincipen) gömde sig i Heisenbergs ursprungliga ekvationer.

Heisenberg hade tittat på de förändringar som sker i en atom när en elektron ändrar sin energinivå och på så sätt närmar sig atomens centrum eller kommer längre bort från centrum, och framför allt på situationer där en elektron faller till ett lägre energitillstånd i två steg. Max Born förklarade hur han tog Heisenbergs märkliga "recept" för att hitta produkten, C, av en viss förändring i en atom från energinivå n till energinivå n-b, vilket innebar att man tog summan av multiplikationen av en förändring i något som kallas A (som till exempel skulle kunna vara frekvensen av en foton) som produceras av en energiväxling av en elektron i atomen mellan energitillstånd n och energitillstånd n-a) med en efterföljande förändring i något som kallas B (som till exempel skulle kunna vara amplituden av en förändring) som produceras av en annan förändring i energitillståndet från n-a till n-b):

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\}\,A(n,n-a)B(n-a,n-b)}

och upptäckte något banbrytande:

Genom att ta hänsyn till ...exempel...[Heisenberg] fann denna regel.... Detta var sommaren 1925. Heisenberg ... tog tjänstledigt ... och överlämnade sin uppsats till mig för publicering....

Heisenbergs multiplikationsregel gav mig ingen ro, och efter en veckas intensivt tänkande och prövande kom jag plötsligt ihåg en algebraisk teori.... Sådana kvadratiska matriser är ganska bekanta för matematiker och kallas matriser, i samband med en bestämd multiplikationsregel. Jag tillämpade denna regel på Heisenbergs kvanttillstånd och fann att den stämde för diagonalelementen. Det var lätt att gissa vad de återstående elementen måste vara, nämligen noll, och omedelbart stod den märkliga formeln framför mig.

Q P - P Q = i h 2 π {\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}
 [Symbolen Q är matrisen för förskjutning, P är matrisen för rörelsemängd, i står för kvadratroten av negativ ett och h är Plancks konstant.]

Senare satte Heisenberg sin upptäckt i en annan matematisk form:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x\,\Delta p\geq {\frac {\hbar }{2}}}

(Den speciella symbolen ℏ {\displaystyle {\hbar }} kallas "h-bar" eller "reducerad Planks-konstant" och är lika med h 2 π {\displaystyle {\frac {h}{2\pi }}} .)

Matematiken är ett sätt att beskriva saker som händer i den verkliga världen. Man kan tänka sig att det skulle vara lätt att få fram både den exakta positionen för något och dess exakta massa, bana och hastighet på samma gång. I verkligheten måste du dock göra två saker för att få ditt svar. Om du mäter positionen och rörelsemängden hos en kula som sitter fast i en klippa på ett stort berg någonstans är det en enkel sak. Berget verkar inte röra sig någonstans, och det gör inte kulan heller. Så dess position är känd och dess hastighet är 0, så dess rörelsemängd är också 0. Men om kulan befinner sig någonstans mellan en pistol och ett mål är det svårt att få fram dess position vid varje given tidpunkt. Det bästa vi kan göra är att ta en bild av den med hjälp av en kamera med mycket snabb slutare. Men ett enda tryck på slutaren skulle bara ge oss en sak, nämligen kulans position vid tiden t. För att få fram impulsen kan vi kanske sätta ett paraffinblock i vägen för kulan och mäta hur paraffinblocket rörde sig när det stoppade kulan. Eller, om vi kände till kulans massa, skulle vi kunna ta en sekvens av två bilder och beräkna hastigheten genom att känna till skillnaden mellan kulans två positioner och tiden mellan dess två framträdanden. Hur vi än gör det måste vi mäta massa, position och tid mellan två framträdanden. Det slutar med att vi gör minst två mätningar för att få fram x och p. I så fall måste vi välja vilken mätning vi ska göra först och vilken vi ska göra sedan. Det verkar inte spela någon roll i vilken ordning våra mätningar görs. Att mäta kulans massa och sedan mäta dess positioner två gånger, eller att mäta kulans positioner två gånger och sedan återta kulan och mäta dess massa skulle väl inte göra någon skillnad? När allt kommer omkring har vi inte gjort något med kulan när vi väger den eller när vi fotograferar den.

På den mycket lilla skalan när vi mäter något som en elektron gör dock varje mätning något med den. Om vi först mäter positionen ändrar vi dess momemtum i processen. Om vi mäter elektronens momentum först, ändrar vi dess position i processen. Vår förhoppning skulle vara att mäta en av dem och sedan mäta den andra innan något förändrades, men vår mätning i sig själv gör en förändring, och det bästa vi kan hoppas på är att minska den energi som vi bidrar till elektronen genom att mäta den till ett minimum. Denna minimala mängd energi har Planckkonstanten som en av sina faktorer.

 

Osäkerheten går bortom matrismatematiken

Heisenbergs osäkerhetsprincip återfanns i de tidigaste ekvationerna i den "nya" kvantfysiken, och teorin gavs med hjälp av matrismatematik. Osäkerhetsprincipen är dock ett faktum om naturen, och den dyker upp i andra sätt att tala om kvantfysik, t.ex. i Erwin Schrödingers ekvationer.

 

Naturens obestämdhet, inte människans osäkerhet

Det har funnits två mycket olika sätt att se på Heisenbergs upptäckt: Vissa människor anser att saker som händer i naturen är "bestämda", det vill säga att saker och ting händer enligt en bestämd regel och att om vi kunde veta allt vi behöver veta skulle vi alltid kunna säga vad som kommer att hända härnäst. Andra anser att saker som händer i naturen endast styrs av sannolikhet och att vi endast kan veta hur saker och ting kommer att bete sig i genomsnitt - men det vet vi mycket exakt.

Fysikern John Stewart Bell upptäckte ett sätt att bevisa att det första sättet inte kan vara korrekt. Hans arbete kallas Bells sats eller Bells ojämlikhet.

 

Populärkultur

Uttrycket "kvantsprång" eller "kvanthopp" har använts för att beteckna en stor och omvälvande förändring, och det används ofta i hyperboliska uttryck av politiker och i massmediernas försäljningskampanjer. Inom kvantmekaniken används det för att beskriva en elektrons övergång från en omloppsbana runt en atomkärna till någon annan omloppsbana, högre eller lägre.

Ibland används ordet "quantum" i namnen på kommersiella produkter och företag. Briggs and Stratton tillverkar till exempel många typer av små bensinmotorer för gräsklippare, rotorklippare och andra små maskiner. Ett av deras modellnamn är "Quantum".

Eftersom osäkerhetsprincipen säger oss att vissa mätningar på atomnivå inte kan göras utan att störa andra mätningar, använder vissa personer denna idé för att beskriva fall i människovärlden där en observatörs aktivitet förändrar det som observeras. En antropolog kan åka till en avlägsen plats för att lära sig hur människor lever där, men det faktum att en främmande person från omvärlden är där och iakttar dem kan förändra hur dessa människor agerar.

Saker som människor gör när de observerar saker som förändrar det som observeras är exempel på observatörseffekten. Vissa saker som människor gör orsakar förändringar på den mycket lilla nivån av atomer och är fall av osäkerhet eller obestämdhet som först beskrevs av Heisenberg. Osäkerhetsprincipen visar att det alltid finns en gräns för hur små vi kan göra vissa par av mätningar, t.ex. position och hastighet eller bana och rörelsekraft. Observatörseffekten säger att ibland kan det som människor gör när de observerar saker, t.ex. att lära sig om en myrstack genom att gräva upp den med trädgårdsredskap, få stora effekter som förändrar det som de försökte lära sig om.