Exponentialfunktion | funktion som växer snabbare och snabbare
Inom matematiken är exponentialfunktionen en funktion som växer allt snabbare. Mer exakt är det funktionen 
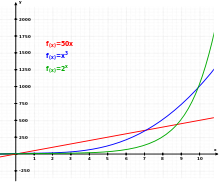
Tre olika funktioner: Linjär (röd), kubisk (blå) och exponentiell (grön).
Egenskaper
Eftersom exponentialfunktioner använder exponentiering följer de samma exponentregler. Således,

Detta följer regeln att 
Den naturliga logaritmen är den omvända operationen av en exponentialfunktion, där:
Exponentialfunktionen uppfyller en intressant och viktig egenskap inom differentialräkning:
Detta innebär att exponentialfunktionens lutning är själva exponentialfunktionen och att den därför har en lutning på 1 vid 
Applikationer
Den allmänna exponentialfunktionen, där basen inte nödvändigtvis är 
Ett exempel på en exponentiell funktion i verkligheten är räntan på en bank. Om en person sätter in 100 pund på ett konto som får 3 % ränta per månad, skulle saldot varje månad (om pengarna inte rörs) se ut på följande sätt:
| Månad | Balans | Månad | Balans |
| Januari | £100.00 | Juli | £119.41 |
| Februari | £103.00 | Augusti | £122.99 |
| Mars | £106.09 | September | £126.68 |
| April | £109.27 | Oktober | £130.48 |
| Maj | £112.55 | November | £134.39 |
| Juni | £115.93 | December | £138.42 |
Lägg märke till att räntekostnaden ökar varje månad, eftersom räntan ökar ju större det ursprungliga saldot är, desto mer ränta får personen.
Två matematiska exempel på exponentialfunktioner (med basen a) visas nedan.
| a=2
| a=3
|
Relation till den matematiska konstanten e
Även om basen ( 
Talet e är viktigt för varje exponentialfunktion. En bank betalar till exempel en ränta på 0,01 procent varje dag. En person tar sina räntepengar och lägger dem i en låda. Efter 10 000 dagar (cirka 30 år) har han 2 gånger så mycket pengar som han började med. En annan person tar sina räntepengar och sätter tillbaka dem på banken. Eftersom banken nu betalar honom ränta på hans ränta är penningmängden en exponentiell funktion.
Efter 10 000 dagar har han faktiskt inte två gånger så mycket pengar som han började med, utan 2,718145 gånger så mycket pengar som han började med. Detta tal ligger mycket nära talet e. Om banken betalar ränta oftare, så att det belopp som betalas ut varje gång är mindre, kommer talet att ligga närmare talet e.
Man kan också titta på bilden för att se varför talet e är viktigt för exponentialfunktioner. Bilden visar tre olika kurvor. Kurvan med de svarta punkterna är en exponentialfunktion med en bas som är något mindre än e. Kurvan med de korta svarta linjerna är en exponentialfunktion med en bas som är något större än e. Den blå kurvan är en exponentialfunktion med en bas som är exakt lika med e. Den röda linjen är en tangent till den blå kurvan. Den berör den blå kurvan i en punkt utan att korsa den. En person kan se att den röda kurvan korsar x-axeln, linjen som går från vänster till höger vid -1. Detta gäller bara för den blå kurvan. Detta är anledningen till att exponentialfunktionen med basen e är speciell.
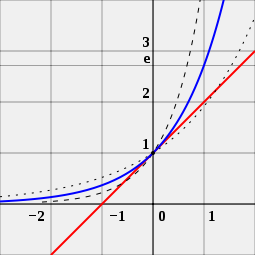
e är det unika talet a som gör att värdet av derivatan av exponentialfunktionen f (x) = ax (blå kurva) i punkten x = 0 är exakt 1. Som jämförelse visas funktionerna 2x (streckad kurva) och 4x (streckad kurva); de tangerar inte linjen med lutningen 1 (röd).
Relaterade sidor
Frågor och svar
F: Vad är exponentialfunktionen?
S: Exponentialfunktionen är en matematisk funktion som växer allt snabbare.
F: Hur uttrycks exponentialfunktionen matematiskt?
S: Exponentialfunktionen uttrycks matematiskt som exp(x) = e^x, där e är Eulers konstant.
F: Vad representerar Eulers konstant?
S: Eulers konstant är ett irrationellt tal som är ungefär 2,71828.
Fråga: Är exponentialfunktionen alltid ökande?
S: Ja, exponentialfunktionen ökar alltid i värde när x ökar.
F: Finns det någon gräns för hur snabbt exponentialfunktionen kan växa?
Svar: Nej, det finns ingen gräns för hur snabbt exponentialfunktionen kan växa eftersom den fortsätter att öka med större värden på x.
F: Hur kan vi beräkna Eulers konstant?
S: Vi kan beräkna Eulers konstant genom att använda numeriska metoder som Taylor-serier eller fortsatta bråk.
F: Vilka andra användningsområden finns det för exponentialfunktionen förutom matematik?
S: Exponentialfunktionen har många tillämpningar utanför matematiken, bland annat inom fysik, kemi, biologi, ekonomi och teknik.
Sök


