Differentialräkning | studiet av att ta reda på förändringshastigheten för en variabel

Differentialräkning, en gren av kalkyl, är en studie av hur man med hjälp av funktioner kan ta reda på förändringshastigheten för en variabel jämfört med en annan variabel. Det är ett sätt att ta reda på hur en form förändras från en punkt till en annan, utan att man behöver dela upp formen i oändligt många delar. Differentialräkning är motsatsen till integralräkning. Den utvecklades på 1670- och 1680-talen av Sir Isaac Newton och Gottfried Leibniz.

Bakgrund

Till skillnad från ett tal som 5 eller 200 kan en variabel ändra sitt värde. Till exempel är avstånd och tid variabler. Vid en olympisk löpartävling ökar avståndet från startlinjen när en person springer. Samtidigt mäter ett stoppur eller en klocka tiden när den ökar. Vi kan mäta löparens genomsnittshastighet om vi delar avståndet som de färdades med den tid det tog. Men detta säger inte vilken hastighet personen sprang med exakt 1,5 sekunder in i loppet. Om vi hade avståndet vid 1 sekund och avståndet vid 2 sekunder skulle vi fortfarande bara ha ett genomsnitt, även om det förmodligen skulle vara mer korrekt än genomsnittet för hela loppet.

Innan kalkylen uppfanns var det enda sättet att räkna ut detta att dela upp tiden i allt mindre bitar, så att medelhastigheten under den mindre tiden skulle komma allt närmare den faktiska hastigheten vid exakt 1,5 sekunder. Detta var en mycket lång och svår process, och måste göras varje gång människor ville räkna ut något. Det är förvisso mycket svårare för en förare att räkna ut en bils hastighet med hjälp av enbart kilometerräknare och klocka - utan hastighetsmätare.

Ett mycket liknande problem är att hitta lutningen (hur brant den är) i en punkt på en kurva. Lutningen på en rät linje är lätt att räkna ut - den är helt enkelt hur mycket den går uppåt (y eller vertikalt) dividerat med hur mycket den går tvärs över (x eller horisontellt). Om en linje är parallell med x-axeln är lutningen noll. Om en rät linje går genom (x,y) = (2,10) och (4,18) går linjen upp 8 och över 2, så dess lutning är 8 dividerat med 2, vilket är 4.

På en "kurva" är lutningen dock en variabel (har olika värden i olika punkter) eftersom linjen böjer sig. Men om kurvan skulle skäras i mycket, mycket små bitar skulle kurvan i punkten nästan se ut som en mycket kort rät linje. Så för att räkna ut dess lutning kan man dra en rät linje genom punkten med samma lutning som kurvan i den punkten. Om det görs exakt rätt kommer den raka linjen att ha samma lutning som kurvan, och kallas en tangent. Men det finns inget sätt att veta (utan kalkyl) om tangenten är exakt rätt, och våra ögon är inte tillräckligt noggranna för att vara säkra på om den är exakt eller bara mycket nära.

Newton och Leibniz fann ett sätt att räkna ut lutningen (eller hastigheten i exemplet med avstånd) exakt, med hjälp av enkla och logiska regler. De delade upp kurvan i ett oändligt antal mycket små bitar. De valde sedan ut punkter på vardera sidan av den punkt som de var intresserade av och räknade ut tangenter vid varje punkt. När punkterna närmade sig varandra mot den punkt som de var intresserade av närmade sig lutningen ett visst värde eftersom tangenterna närmade sig kurvans verkliga lutning. De sa att detta särskilda värde som närmade sig var den verkliga lutningen.

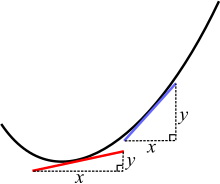
På en kurva har två olika punkter olika lutning. De röda och blå linjerna är tangenter till kurvan.

Hur det fungerar

Låt oss säga att vi har en funktion y = f(x). f är en förkortning för funktion, så denna ekvation betyder "y är en funktion av x". Detta säger oss att hur högt y är på den vertikala axeln beror på vad x (den horisontella axeln) är vid den tidpunkten. Med ekvationen y = x² vet vi t.ex. att om x är 1 kommer y att vara 1, om x är 3 kommer y att vara 9 och om x är 20 kommer y att vara 400.

Välj en punkt A på kurvan och kalla dess horisontella position x. Välj sedan en annan punkt B på kurvan som ligger lite längre bort än A och kalla dess horisontella position x + h. Det spelar ingen roll hur mycket h är; det är ett mycket litet tal.

Så när vi går från punkt A till punkt B har den vertikala positionen gått från f(x) till f(x + h) och den horisontella positionen har gått från x till x + h. Kom ihåg att lutningen är hur mycket det går uppåt dividerat med hur mycket det går över. Så lutningen blir:

f ( x + h ) - f ( x ) h {\displaystyle {\frac {f(x+h)-f(x)}{h}}} ${\frac {f(x+h)-f(x)}{h}}$

Om du för B närmare och närmare A - vilket innebär att h närmar sig 0 - kommer vi närmare att veta hur lutningen är vid punkten A.

lim h → 0 f ( x + h ) - f ( x ) h {\displaystyle \lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}} $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}$

Låt oss nu gå tillbaka till y = x². Lutningen kan bestämmas på följande sätt:

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}}{h}}\end{aligned}}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}$

Genom att tillämpa binomialsatsen som delvis säger att ( x + y ) 2 = x 2 + 2 x y + y 2 {\displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}} $(x+y)^{2}=x^{2}+2xy+y^{2}$ kan vi reducera uttrycket till:

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}}{h}}\&=\lim _{h\rightarrow 0}2x+h\\\&={\frac {}{}}2x\end{aligned}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}$

Vi vet alltså utan att behöva rita några tangenter att i varje punkt på kurvan f(x) = x² kommer derivatan f'(x) (markerad med apostrof) att vara 2x i varje punkt. Denna process att räkna ut en lutning med hjälp av gränser kallas differentiering eller att hitta derivatan.

Leibniz kom fram till samma resultat, men kallade h för "dx", vilket betyder "en liten mängd x". Han kallade den resulterande förändringen av f(x) för "dy", vilket betyder "en liten del av y". Leibniz' notation används i fler böcker eftersom den är lätt att förstå när ekvationerna blir mer komplicerade. I Leibniz notation:

d y d x = f ′ ( x ) {\displaystyle {\frac {dy}{dx}}=f'(x)} ${\frac {dy}{dx}}=f'(x)$

En bild som visar vad x och x + h betyder på kurvan.

Regler

Med hjälp av ovanstående system har matematikerna utarbetat regler som fungerar hela tiden, oavsett vilken funktion man tittar på. (Obs: här är u {\displaystyle u} $u$ och v {\displaystyle v} $v$ båda funktioner av x {\displaystyle x} )

Villkor	Funktion	Derivat	Exempel	Derivat
En siffra i sig själv	y = a {\displaystyle y=a} $y=a$	d y d x = 0 {\displaystyle {\frac {dy}{dx}}=0}} ${\frac {dy}{dx}}=0$	y = 3 {\displaystyle y=3} $y=3$	0 {\displaystyle 0} $0$
En rak linje	y = m x + c {\displaystyle y=mx+c} $y=mx+c$	d y d x = m {\displaystyle {\frac {dy}{dx}}=m} ${\frac {dy}{dx}}=m$	y = 3 x + 5 {\displaystyle y=3x+5} $y=3x+5$	3 {\displaystyle 3} $3$
x till potensen av ett tal	x a {\displaystyle x^{a}} $x^{a}$	d y d x = a x a - 1 {\displaystyle {\frac {dy}{dx}}=ax^{a-1}}} ${\frac {dy}{dx}}=ax^{a-1}$	x 12 {\displaystyle x^{12}} $x^{12}$	12 x 11 {\displaystyle 12x^{11}} $12x^{11}$
Ett tal multiplicerat med en funktion	y = c ⋅ u {\displaystyle y=c\cdot u} $y=c\cdot u$	d y d x = c d u d x {\displaystyle {\frac {dy}{dx}}}=c{\frac {du}{dx}}} ${\frac {dy}{dx}}=c{\frac {du}{dx}}$	y = 3 ( x 2 + x ) {\displaystyle y=3(x^{2}+x)} $y=3(x^{2}+x)$	3 ( 2 x + 1 ) {\displaystyle 3(2x+1)} $3(2x+1)$
En funktion plus en annan funktion	y = u + v {\displaystyle y=u+v} $y=u+v$	d y d x = d u d x + d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}}+{\frac {dv}{dx}}} ${\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}$	y = 3 x 2 + x {\displaystyle y=3x^{2}+{\sqrt {x}}} $y=3x^{2}+{\sqrt {x}}$	6 x + 1 2 x {\displaystyle 6x+{\frac {1}{2{\sqrt {x}}}}} $6x+{\frac {1}{2{\sqrt {x}}}}$
En funktion minus en annan funktion	y = u - v {\displaystyle y=u-v} $y=u-v$	d y d x = d u d x - d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}}-{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}$	y = 3 x 2 - x {\displaystyle y=3x^{2}-{\sqrt {x}}} $y=3x^{2}-{\sqrt {x}}$	6 x - 1 2 x {\displaystyle 6x-{\frac {1}{2{\sqrt {x}}}}} $6x-{\frac {1}{2{\sqrt {x}}}}$
Produktregel En funktion multiplicerad med en annan funktion	y = u ⋅ v {\displaystyle y=u\cdot v} $y=u\cdot v$	d y d x = d u d x v + u d v d x {\displaystyle {\frac {dy}{dx}}}={\frac {du}{dx}}}v+u{\frac {dv}{dx}}} ${\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}$	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {\displaystyle y=(x^{2}+x+2)(3x-1)} $y=(x^{2}+x+2)(3x-1)$	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) {\displaystyle (3x-1)(2x+1)+3(x^{2}+x+2)} $(3x-1)(2x+1)+3(x^{2}+x+2)$
Kvotregeln En funktion dividerad med en annan funktion	y = u v {\displaystyle y={\frac {u}{v}}}} $y={\frac {u}{v}}$	d y d x = d u d x v - u d v d x v 2 {\displaystyle {\frac {dy}{dx}}={\frac {{\frac {{\frac {du}{dx}}}v-u{\frac {dv}{dx}}}{v^{2}}}} ${\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}$	y = x 2 + 2 x - 1 {\displaystyle y={\frac {x^{2}+2}{x-1}}}} $y={\frac {x^{2}+2}{x-1}}$	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {\displaystyle {\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}} ${\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}$
Kedjeregel Används för sammansatta funktioner	y = u ∘ v {\displaystyle y=u\circ v} $y=u\circ v$	d y d x = d y d u ⋅ d u d x {\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}}\cdot {\frac {du}{dx}}}} ${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$	y = 2 x - 1 {\displaystyle y={\sqrt {2x-1}}} $y={\sqrt {2x-1}}$	2 2 2 2 x - 1 = 1 2 x - 1 {\displaystyle {\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}} ${\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}$
En exponentialfunktion	y = e x {\displaystyle {\frac {}{}}}y=e^{x}} ${\frac {}{}}y=e^{x}$	d y d x = e x {\displaystyle {\frac {dy}{dx}}=e^{x}} ${\frac {dy}{dx}}=e^{x}$	y = e x {\displaystyle {\frac {}{}}}y=e^{x}} ${\frac {}{}}y=e^{x}$	e x {\displaystyle {\frac {}{}}}e^{x}} ${\frac {}{}}e^{x}$

Relaterade sidor

Derivat (matematik)
Differentialoperator
Ordinära differentialekvationer
Matematisk analys

Frågor och svar

F: Vad är differentialräkning?

S: Differentialräkning är en gren av kalkyl som studerar förändringshastigheten hos en variabel jämfört med en annan variabel, med hjälp av funktioner.

F: Hur fungerar det?

S: Differentialräkning gör det möjligt för oss att ta reda på hur en form förändras från en punkt till en annan utan att behöva dela upp formen i ett oändligt antal delar.

F: Vem utvecklade differentialräkning?

S: Differentialräkning utvecklades på 1670- och 1680-talen av Sir Isaac Newton och Gottfried Leibniz.

F: Vad är integralkalkyl?

S: Integralkalkyl är motsatsen till differentialkalkyl. Den används för att hitta areor under kurvor och volymer av fasta kroppar med krökta ytor.

F: När utvecklades differentialräkning?