AlegsaOnline.com

Gumbelfördelningen – definition, egenskaper och tillämpningar för extrema värden

Gumbelfördelningen: förklaring, egenskaper och praktiska tillämpningar för extrema värden — modellera översvämningar, jordbävningar och riskbedömningar med statistiska metoder.

Författare: Leandro Alegsa

09-10-2025

Gumbelfördelningen är en sannolikhetsfördelning av extrema värden.

Inom sannolikhetsteori och statistik används Gumbelfördelningen för att modellera fördelningen av maximum (eller minimum) för ett antal prov av olika fördelningar.

En sådan fördelning skulle kunna användas för att representera fördelningen av den högsta nivån i en flod under ett visst år om det finns en förteckning över de högsta nivåerna under de senaste tio åren. Den är också användbar för att förutsäga chansen att en extrem jordbävning, översvämning eller annan naturkatastrof kommer att inträffa.

Vad är Gumbelfördelningen?

Gumbelfördelningen (även kallad extremvärdesfördelning typ I) beskriver fördelningen av extremvärden, vanligtvis maxima, i en sekvens av oberoende och identiskt fördelade slumpvariabler när provstorleken blir stor. Den uppstår som ett gränsvärde i extremvärdeteorin och är en speciell fall av den generaliserade extremvärdesfördelningen (GEV) med formparameter ξ = 0.

Matematisk form

För parametrarna läge μ (mu) och skala β (beta > 0) ges fördelningsfunktionen (CDF) och täthetsfunktionen (PDF) av:

CDF: F(x) = exp(−exp(−(x − μ)/β)).
PDF: f(x) = (1/β) · exp(−(x − μ)/β) · exp(−exp(−(x − μ)/β)).

För att simulera ett Gumbel-prov kan man använda invers transform: om U ~ Uniform(0,1) så ges X = μ − β ln(−ln(U)). För att modellera minima används ofta den speglade varianten (negativ Gumbel) eller motsvarande parameterisering.

Egenskaper och centrala mått

Medelvärde: E[X] = μ + γ β, där γ ≈ 0,5772156649 är Eulers konstant (Euler–Mascheroni).
Varians: Var(X) = (π²/6) β².
Skewness (skevhet): ≈ 1,139547 (oberoende av μ, proportionell i skala).
Kurtosis (översta): excess kurtosis ≈ 12/5 = 2,4.
Halen: Gumbel har en exponentiellt avtagande högersvans; asymptotiskt beter sig överlevnadsfunktionen som ~ exp(−(x − μ)/β) för stora x, dvs. svansen är av typ "light tail" jämfört med kraftlagar.

Tillämpningar

Gumbelfördelningen används i många praktiska områden där extrema observationer är intressanta:

Hydrologi: modellera årsmaxima för flodnivåer för översvämningsrisk och bestämma återkommande nivåer (t.ex. 100-årsflod).
Meteorologi: vindhastigheter, dagliga temperaturextremer, nederbördstopp.
Geovetenskap: starkaste jordbävningar eller största skred.
Teknisk tillförlitlighet och säkerhetsberäkningar: dimensionera konstruktioner för extrem belastning.
Finans: modellera extrema förluster (med försiktighet — ofta används andra tungsvansade modeller där lämpligt).

Återkomstnivåer (return levels)

För att bedöma hur stort ett extremt utfall med låg sannolikhet kan bli använder man begreppet återkomstnivå. Om p är sannolikheten att en observation inte överskrids (dvs. F(z_p) = p) är lösningen

z_p = μ − β ln(−ln p).

Vid praktiska beräkningar är man intresserad av p = 1 − 1/T där T är återkomstperioden (t.ex. T = 100 år). Då fås den T-åriga återkomstnivån z_{1−1/T} = μ − β ln(−ln(1 − 1/T)).

Parameterestimering

Vanliga metoder för att skatta μ och β:

Maximalloglikhet (MLE): leder normalt till icke-linjära ekvationer som löses numeriskt. MLE är effektiv när antalet observationer inte är alltför litet.
Metod av moment: man kan uppskatta β från variansen: β̂ = sqrt(6·s²)/π och därefter μ̂ = x̄ − γ β̂, där x̄ är stickprovsmedel och s² stickprovsvarians.
L-momentmetoder: ofta använda inom extremvärdesanalys eftersom de är robusta mot outliers och små provstorlekar.

Vid verkliga data bör man också undersöka antagandet om oberoende och stationäritet samt eventuellt modellera trender eller icke-stationära parametrar.

Relationer och alternativa modeller

Gumbel är ett specialfall av den generaliserade extremvärdesfördelningen (GEV) med formparameter ξ = 0.
Andra extremvärdesfördelningar är Fréchet (ξ > 0) för tungsvansade data och Weibull/negativ Weibull (ξ < 0) för begränsade övre gränser.
För vissa typer av data kan andra modeller (t.ex. t-fördelningar, Pareto) vara mer lämpliga om man observerar mycket tungsvansade fenomen.

Praktiska råd vid användning

Kontrollera att data representerar jämförbara block (t.ex. årsmaxima) och att observationerna är tillräckligt många och oberoende.
Gör diagnostiska plottar: QQ-plot mot teoretisk Gumbel, plott av återkomstnivåer, residualanalyser.
Använd flera estimeringsmetoder (MLE, L-moments) och jämför resultat för stabilitet.
Tänk på osäkerheten: ange konfidensintervall för återkomstnivåer och parametrar, särskilt för låga frekvenser (långa återkomstperioder) där osäkerheten ökar kraftigt.

Programvara och simulering

Gumbel-modeller kan fitas och simuleras i de flesta statistikpaket. Exempel:

Använd invers transform X = μ − β ln(−ln(U)) för simulering med U ~ Uniform(0,1).
I statistikprogram som R finns paket och funktioner för extremvärdesanalys (t.ex. paket för GEV/Gumbel, L-moments och MLE). I Python kan man använda scipy.stats.gumbel_r (eller motsvarande) för att passa och simulera data.

Begränsningar

Gumbel antas ofta som modell för maxima men passar inte alltid; om data visar mycket tung svans kan en Fréchet-typ vara bättre.
Om data inte är stationära (t.ex. klimattrender) måste parametrarna göras beroende av tid eller annan covariat för att få meningsfulla prognoser.
Små provstorlekar leder till stor osäkerhet i extrema kvantiler; tolka därför långtidsprognoser försiktigt.

Sammanfattningsvis är Gumbelfördelningen ett användbart och välstuderat verktyg inom extremvärdesanalys, lämpligt när extrema maxima eller minima ska modelleras under antagandet av exponentiallyt beteende i svansarna. Val av modell och estimeringsmetod bör dock alltid anpassas efter data och syftet med analysen.

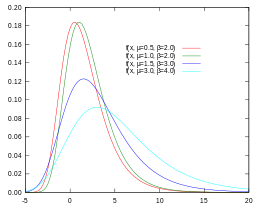
Gumbels sannolikhetsfördelningsfunktion (PDF)

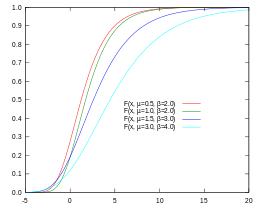
Gumbel kumulativ fördelningsfunktion (CDF)

Egenskaper

Gumbelfördelningen är en kontinuerlig sannolikhetsfördelning. Gumbelfördelningar är en familj av fördelningar av samma allmänna form. Dessa fördelningar skiljer sig åt genom sina parametrar för läge och skala: fördelningens medelvärde ("genomsnitt") definierar dess läge, och standardavvikelsen ("variabilitet") definierar skalan.

Man känner igen Gumbels sannolikhetsdensitetsfunktion (PDF) och Gumbels kumulativa distributionsfunktion (CDF).

PDF

I PDF-analysen beräknas sannolikheten P för att ett värde V ska inträffa mellan gränserna A och B, kortfattat uttryckt som P(A<V<B), genom arean under PDF-kurvan mellan A och B.

Exempel på sannolikhet i PDF-filen

I figuren över den normala sannolikhetsdensitetsfunktionen ska värdena på den horisontella axeln vara: μ-3σ, μ-2σ, μ-1σ, μ+1σ, μ+2σ respektive μ+3σ.

μ = medelvärde, σ = standardavvikelse.
Områdena under kurvan i intervallerna, vart och ett med en bredd av en standardavvikelse, ger sannolikheten för förekomst i dessa intervall.
Exempel: Sannolikheten för att ett värde V ska inträffa i intervallet mellan A=μ+1σ och B=μ+2σ är P(μ+1σ<V<μ+2σ)=13,6 % eller 0,136.

I motsats till normalfördelningen är Gumbels PDF-dokument a-symmetriskt och snett åt höger.

CDF

I CDF-analysen är sannolikheten för att ett värde V är mindre än A direkt lika med CDF-värdet vid A:

P ( V ≤ A ) = C D F ( A ) {\displaystyle P(V\leq A)=CDF(A)} $P(V\leq A)=CDF(A)$ .

Exempel på sannolikhet i CDF

I Gumbels CDF-figur visar den röda kurvan att sannolikheten för att V är mindre än 5 är 0,9 (eller 90 %), medan sannolikheten för den mörkblå linjen är 0,7 eller 70 %.

Den normala sannolikhetstäthetsfunktionen (PDF) är symmetrisk.

Matematik

CDF

Det matematiska uttrycket för CDF är:

C D F ( A ) = e - e - ( A - μ ) / β , {\displaystyle CDF(A)=e^{-e^{-(A-\mu )/\beta }},} $CDF(A)=e^{-e^{-(A-\mu )/\beta }},$

där μ är modus (det värde där sannolikhetstäthetsfunktionen når sin topp), e är en matematisk konstant, cirka 2,718, och β är ett värde relaterat till standardavvikelsen (σ) :

β = σ 6 / π , {\displaystyle \beta =\sigma {\sqrt {6}}}/\pi ,} $\beta =\sigma {\sqrt {6}}/\pi ,$

där π är den grekiska symbolen för Pi vars värde ligger nära 22/7 eller 3,142, och symbolen {\displaystyle {\sqrt {\,\,}}} ${\sqrt {\,\,}}$ står för kvadratroten.

Mode och median

Modus μ kan hittas från medianen M, som är värdet av A där CDF(A)=0,5 och β:

μ = M + β ln ( ln 2 ) , {\displaystyle \mu = M+\beta \ln \ vänster(\ln 2\ höger),} $\mu =M+\beta \ln \left(\ln 2\right),$

där ln är den naturliga logaritmen.

Medelvärde

Medelvärdet, E(x), ges av:

E ( x ) = μ + c β , {\displaystyle \operatorname {E} (x)=\mu +c\beta ,} $\operatorname {E} (x)=\mu +c\beta ,$

där c {\displaystyle c} $c$ = Eulerkonstant ≈ {\displaystyle \approx } $\approx$ 0.5772.

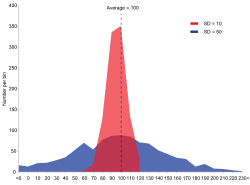
Det finns två dataserier: röd och blå. Båda har samma medelvärde (genomsnitt): 100, men den blå gruppen har en större standardavvikelse (SD=σ=50) än den röda gruppen (SD=σ=10).

Uppskattning

I en dataserie kan parametrarna mode (μ) och β uppskattas från genomsnittet, medianen och standardavvikelsen. Beräkningen av de tre sistnämnda storheterna förklaras på respektive Wikisidor. Därefter kan faktorerna μ och β beräknas med hjälp av de formler som anges i föregående avsnitt. På detta sätt kan CDF för den Gumbelfördelning som hör till uppgifterna bestämmas och sannolikheten för intressanta datavärden kan hittas.

Anpassad kumulativ Gumbel-fördelning för de största regnmängderna under en dag i oktober med hjälp av CumFreq.

Ansökan

Inom hydrologin används Gumbelfördelningen för att analysera variabler som månads- och årsmaximumvärden för daglig nederbörd och flodavrinningsvolymer, och även för att beskriva torka.

Den blå bilden visar ett exempel på anpassning av Gumbelfördelningen till de rangordnade maximala regnmängderna under en dag i oktober och visar även det 90-procentiga konfidensbältet baserat på binomialfördelningen.

Frågor och svar

F: Vad är Gumbel-fördelningen?

S: Gumbelfördelningen är en sannolikhetsfördelning av extremvärden.

F: Vad används Gumbel-fördelningen till?

S: Gumbelfördelningen används för att modellera fördelningen av det maximala (eller det minimala) värdet i ett antal stickprov av olika fördelningar.

F: Hur kan Gumbel-fördelningen användas för att förutsäga naturkatastrofer?

S: Gumbelfördelningen är användbar för att förutsäga risken för att en extrem jordbävning, översvämning eller annan naturkatastrof ska inträffa.

F: Vad är ett exempel på hur Gumbelfördelningen kan användas för att representera en tidigare händelse?

S: Gumbelfördelningen skulle kunna användas för att representera fördelningen av den högsta nivån i en flod under ett visst år om det fanns en lista över högsta värden för de senaste tio åren.

F: Är Gumbelfördelningen bara användbar för att förutsäga naturkatastrofer?

S: Nej, Gumbelfördelningen kan användas för att modellera fördelningen av extrema värden i alla situationer.

F: Kan Gumbel-fördelningen användas för att modellera det lägsta värdet i en uppsättning stickprov?

S: Ja, Gumbel-fördelningen kan användas för att modellera fördelningen av antingen det maximala eller det minimala värdet i en uppsättning stickprov.

F: Är Gumbel-fördelningen en vanligt förekommande fördelning inom sannolikhetsteori och statistik?

S: Ja, Gumbelfördelningen är en vanligt förekommande fördelning inom sannolikhetsteori och statistik, särskilt för modellering av extremvärden.