Standardavvikelse | ett tal som används för att tala om hur mätningar för en grupp är spridda från genomsnittet
Standardavvikelse är ett tal som används för att ange hur mätningarna för en grupp är spridda från genomsnittet (medelvärdet eller det förväntade värdet). En låg standardavvikelse innebär att de flesta siffrorna ligger nära genomsnittet, medan en hög standardavvikelse innebär att siffrorna är mer utspridda.
Den rapporterade felmarginalen är vanligtvis dubbelt så stor som standardavvikelsen. Forskare rapporterar vanligen standardavvikelsen för tal från det genomsnittliga antalet i experiment. De beslutar ofta att endast skillnader som är större än två eller tre gånger standardavvikelsen är viktiga. Standardavvikelsen är också användbar inom penningområdet, där standardavvikelsen för ränteintäkter visar hur stor skillnaden mellan en persons ränteintäkter och genomsnittet kan vara.
Ofta kan endast ett urval eller en del av en grupp mätas. Då kan ett tal som ligger nära standardavvikelsen för hela gruppen hittas med hjälp av en något annorlunda ekvation som kallas standardavvikelse för stickprov, som förklaras nedan. I detta fall representeras standardavvikelsen för hela gruppen av den grekiska bokstaven 

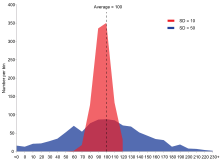
Exempel på två urvalspopulationer med samma medelvärde och olika standardavvikelser. Den röda populationen har medelvärde 100 och SD 10, den blå populationen har medelvärde 100 och SD 50.
.png)
En plott av en normalfördelning (eller en klockkurva). Varje färgat band har en bredd på en standardavvikelse.
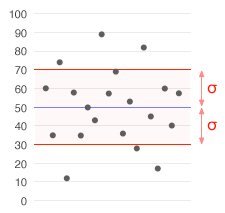
En datamängd med ett medelvärde på 50 (visas i blått) och en standardavvikelse (σ) på 20.
Grundläggande exempel
Tänk på en grupp med följande åtta nummer:
Dessa åtta tal har ett genomsnitt (medelvärde) på 5:
För att beräkna populationens standardavvikelse ska du först ta reda på skillnaden mellan varje tal i listan och medelvärdet. Kvadrera sedan resultatet av varje skillnad:
Därefter tar du fram medelvärdet av dessa värden (summan dividerad med antalet nummer). Slutligen tar du kvadratroten:
Svaret är populationens standardavvikelse. Formeln är bara sann om de åtta siffrorna vi började med utgör hela gruppen. Om de bara är en del av gruppen som valts ut slumpmässigt kan vi få en fördomsfri uppskattning av vad populationens standardavvikelse är genom att dividera med 7 (som är n - 1) i stället för 8 (som är n) i botten (nämnaren) av formeln ovan. Svaret är då den (bias-korrigerade) standardavvikelsen för urvalet. Detta kallas Besselkorrigering. Vi använder ofta denna korrigering eftersom urvalets varians, dvs. kvadraten på urvalets standardavvikelse, är en ofördelaktig skattare av populationsvariansen, med andra ord är det förväntade värdet eller långtidsgenomsnittet av urvalets varians lika med populationens (sanna) varians. Det är dock inte så att urvalets standardavvikelse är en fördomsfri skattning av populationens standardavvikelse. 1 Även om Bessels korrigering är en fördomsfri skattning av variansen har denna skattning ett högre medelkvadratfel än den fördomsfulla skattningen, eller med andra ord, den fördomsfulla skattningen (dvs. att dividera med n i stället för med n-1) ligger i genomsnitt närmare det sanna värdet.
Fler exempel
Här är ett lite svårare exempel från verkligheten: Den genomsnittliga längden för vuxna män i USA är 70", med en standardavvikelse på 3". En standardavvikelse på 3" innebär att de flesta män (ca 68 %, om man utgår från en normalfördelning) har en längd som är 3" längre till 3" kortare än genomsnittet (67"-73") - en standardavvikelse. Nästan alla män (ca 95 %) har en längd som är 6" högre till 6" lägre än genomsnittet (64-76") - två standardavvikelser. Tre standardavvikelser omfattar alla siffror för 99,7 % av den undersökta urvalspopulationen. Detta gäller om fördelningen är normal (klockformad).
Om standardavvikelsen vore noll skulle alla män vara exakt 70 tum långa. Om standardavvikelsen var 20" skulle vissa män vara mycket längre eller mycket kortare än genomsnittet, med ett typiskt intervall på cirka 50"-90".
Ett annat exempel: Var och en av de tre grupperna {0, 0, 14, 14, 14}, {0, 6, 8, 14} och {6, 6, 8, 8} har ett medelvärde på 7. Men deras standardavvikelser är 7, 5 och 1. Den tredje gruppen har en mycket mindre standardavvikelse än de andra två eftersom alla dess siffror ligger nära 7. I allmänhet säger standardavvikelsen hur långt från medelvärdet resten av siffrorna tenderar att ligga, och den kommer att ha samma enheter som siffrorna i sig själva. Om gruppen {0, 6, 8, 14} till exempel är åldrarna för en grupp på fyra bröder i år, är genomsnittet 7 år och standardavvikelsen 5 år.
Standardavvikelsen kan fungera som ett mått på osäkerhet. Inom vetenskapen hjälper till exempel standardavvikelsen för en grupp upprepade mätningar forskarna att veta hur säkra de är på det genomsnittliga antalet. När man beslutar om mätningar från ett experiment stämmer överens med en förutsägelse är standardavvikelsen för dessa mätningar mycket viktig. Om det genomsnittliga antalet från experimenten ligger för långt ifrån det förutspådda antalet (där avståndet mäts i standardavvikelser) kanske teorin som testas inte stämmer. För mer information, se prediktionsintervall.
Exempel på tillämpningar
Genom att förstå standardavvikelsen för en uppsättning värden kan vi veta hur stor skillnad från "genomsnittet" (medelvärdet) som kan förväntas.
Väder
Som ett enkelt exempel kan vi ta den genomsnittliga dagstemperaturen för två städer, en i inlandet och en nära havet. Det är bra att förstå att intervallet av dagliga höga temperaturer för städer nära havet är mindre än för städer i inlandet. Dessa två städer kan ha samma genomsnittliga dagliga höga temperatur. Standardavvikelsen för den dagliga höga temperaturen för kuststaden kommer dock att vara mindre än för staden i inlandet.
Sport
Ett annat sätt att se på saken är att betrakta idrottslag. I alla sporter finns det lag som är bra på vissa saker och inte på andra. De lag som är högst rankade kommer inte att uppvisa så stora skillnader i förmågor. De gör bra ifrån sig i de flesta kategorier. Ju lägre standardavvikelsen för deras förmåga i varje kategori är, desto mer balanserade och konsekventa är de. Lag med en högre standardavvikelse kommer dock att vara mindre förutsägbara. Ett lag som vanligtvis är dåligt i de flesta kategorier kommer att ha en låg standardavvikelse. Ett lag som vanligtvis är bra i de flesta kategorier kommer också att ha en låg standardavvikelse. Ett lag med hög standardavvikelse kan dock vara ett lag som gör många poäng (stark offensiv) men som också låter det andra laget göra många poäng (svagt försvar).
För att försöka veta i förväg vilka lag som kommer att vinna kan man titta på standardavvikelserna för de olika lagens "statistik". Siffror som skiljer sig från det förväntade kan matcha styrkor mot svagheter för att visa vilka skäl som kan vara viktigast för att veta vilket lag som kommer att vinna.
I racing mäts den tid som en förare behöver för att slutföra varje varv runt banan. En förare med en låg standardavvikelse för varvtiderna är mer konsekvent än en förare med en högre standardavvikelse. Denna information kan användas för att hjälpa till att förstå hur en förare kan minska tiden för att avsluta ett varv.
Pengar
I pengar kan standardavvikelse betyda risken för att ett pris kommer att stiga eller sjunka (aktier, obligationer, fastigheter osv.). Det kan också betyda risken för att en grupp av priser kommer att stiga eller sjunka (aktivt förvaltade värdepappersfonder, indexbaserade värdepappersfonder eller ETF:er). Risk är en anledning att fatta beslut om vad man ska köpa. Risk är ett tal som människor kan använda för att veta hur mycket pengar de kan tjäna eller förlora. När risken blir större kan avkastningen på en investering bli större än förväntat (standardavvikelsen "plus"). Men en investering kan också förlora mer pengar än förväntat (standardavvikelsen "minus").
En person måste till exempel välja mellan två aktier. Aktie A har under de senaste 20 åren haft en genomsnittlig avkastning på 10 procent, med en standardavvikelse på 20 procentenheter (pp). Aktie B har under de senaste 20 åren haft en genomsnittlig avkastning på 12 procent men en högre standardavvikelse på 30 procentenheter. När personen tänker på risken kan han eller hon besluta att aktie A är det säkrare valet. Även om de kanske inte tjänar lika mycket pengar kommer de förmodligen inte heller att förlora mycket pengar. Personen kanske anser att aktie B:s 2 procentenheter högre genomsnitt inte är värt den extra standardavvikelsen på 10 procentenheter (större risk eller osäkerhet i fråga om den förväntade avkastningen).
Regler för normalfördelade tal
De flesta matematiska ekvationer för standardavvikelse förutsätter att siffrorna är normalfördelade. Det innebär att siffrorna är spridda på ett visst sätt på båda sidor om medelvärdet. Normalfördelningen kallas också för Gauss-fördelning eftersom den upptäcktes av Carl Friedrich Gauss. Den kallas ofta för klockkurvan eftersom siffrorna sprids ut så att de får formen av en klocka på en graf.
Tal är inte normalfördelade om de är grupperade på ena eller andra sidan av medelvärdet. Siffror kan vara utspridda och ändå vara normalfördelade. Standardavvikelsen anger hur mycket siffrorna är spridda.

Mörkblått är mindre än en standardavvikelse från medelvärdet. För normalfördelningen omfattar detta 68,27 procent av siffrorna, medan två standardavvikelser från medelvärdet (medium och mörkblått) omfattar 95,45 procent, tre standardavvikelser (ljus, medium och mörkblått) omfattar 99,73 procent och fyra standardavvikelser omfattar 99,994 procent.
Förhållandet mellan medelvärde och standardavvikelse
Genomsnittet (medelvärdet) och standardavvikelsen för en uppsättning data skrivs vanligtvis tillsammans. Då kan en person förstå vad det genomsnittliga talet är och hur stor spridning de andra talen i gruppen har.
Hur en grupp siffror är spridda kan också anges med hjälp av variationskoefficienten (CV), som är standardavvikelsen dividerad med genomsnittet. Det är ett dimensionslöst tal. Variationskoefficienten multipliceras ofta med 100 % och skrivs som en procentsats.
Historia
Begreppet standardavvikelse användes för första gången skriftligen av Karl Pearson 1894, efter att han använt det i föreläsningar. Det var som en ersättning för tidigare namn för samma idé: Gauss använde till exempel medelfel.
Relaterade sidor
- Noggrannhet och precision
- Provstorlek
- Standardfel
- Avvikelse
Frågor och svar
F: Vad är standardavvikelse?
S: Standardavvikelse är ett tal som används för att tala om hur mätningar för en grupp är spridda från genomsnittet (medelvärdet eller det förväntade värdet).
F: Vad innebär en låg standardavvikelse?
S: En låg standardavvikelse innebär att de flesta siffrorna ligger nära genomsnittet.
F: Vad innebär en hög standardavvikelse?
S: En hög standardavvikelse innebär att siffrorna är mer utspridda.
F: Hur används standardavvikelse i pengar?
S: I pengar visar standardavvikelsen för ränteintäkter hur mycket en persons ränteintäkter kan skilja sig från genomsnittet.
F: När kan endast en del av en grupp mätas?
S: Många gånger kan endast ett urval eller en del av en grupp mätas.
F: Hur representeras hela gruppens standardavvikelse?
S: Hela gruppens standardavvikelse representeras av den grekiska bokstaven َ {\displaystyle \sigma }. .
F: Hur representeras urvalets standardavvikelse?
S: Provets standardavvikelse representeras av s {\displaystyle s} .
Sök



