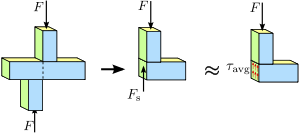Spänning (mekanik) – definition, formel och enheter
Spänning (mekanik): Förklaring, formel σ=F/A, SI-enheten Pascal (Pa), enheter och exempel — allt om krafter per ytenhet och spänningsfördelning.
Spänning är den kraft per ytenhet på en kropp som tenderar att få den att ändra form.
Spänning är ett mått på de inre krafterna i en kropp mellan dess partiklar. Dessa inre krafter är en reaktion på de yttre krafter som tillämpas på kroppen och som får den att separera, komprimeras eller glida. Yttre krafter är antingen ytkrafter eller kroppskrafter. Spänningen är den genomsnittliga kraft per ytenhet som en partikel i en kropp utövar på en intilliggande partikel, över en tänkt yta som skiljer dem åt.
Formeln för enaxlig normalspänning är:
σ = F A {\displaystyle {\sigma }={\frac {F}{A}}}
där σ är spänningen, F är kraften och A är ytan.
I SI-enheter mäts kraften i Newton och arean i kvadratmeter. Detta innebär att spänningen är newton per kvadratmeter, eller N/m2. Spänning har dock en egen SI-enhet som kallas pascal. 1 pascal (symbol Pa) är lika med 1 N/m2. I imperiala enheter mäts spänningen i pundkraft per kvadrattum, vilket ofta förkortas till "psi". Dimensionen för spänning är densamma som för tryck.
I kontinuumsmekaniken beter sig den belastade deformerbara kroppen som ett kontinuum. Dessa inre krafter fördelas alltså kontinuerligt inom den materiella kroppens volym. (Detta innebär att spänningsfördelningen i kroppen uttrycks som en styckevis kontinuerlig funktion av rum och tid). Krafterna orsakar deformation av kroppens form. Deformationen kan leda till en permanent formförändring eller strukturellt brott om materialet inte är tillräckligt starkt.
I vissa modeller av kontinuumsmekanik behandlas kraft som något som kan förändras. Andra modeller tittar på deformationen av materia och fasta kroppar, eftersom materiens och fasta kroppars egenskaper är tredimensionella. Varje tillvägagångssätt kan ge olika resultat. Klassiska modeller för kontinuumsmekanik utgår från en genomsnittlig kraft och tar inte hänsyn till "geometriska faktorer" på ett korrekt sätt. (Kroppens geometri kan vara viktig för hur spänningen fördelas och hur energin byggs upp under utövandet av den yttre kraften).
Typer av spänning
- Normalspänning (σ): verkar vinkelrätt mot en yta. Vid drag kallas den dragspänning, vid tryck kallas den tryckspänning.
- Skjuvspänning (τ): verkar parallellt med ytan och försöker få materialskikten att glida i förhållande till varandra.
- Böjspänning: uppstår när ett element utsätts för böjmoment; för en balk varierar normalspänningen över tvärsnittet och beräknas ofta med σ = M y / I (M = moment, y = avstånd från neutralaxeln, I = tvärsnittets andra moment).
- Torsionsspänning: uppstår i axlar som utsätts för vridmoment; skjuvspänningen i ett cirkulärt tvärsnitt ges av τ = T r / J (T = vridmoment, r = radie, J = polärt tröghetsmoment).
Spänning i punkt och tensorbegreppet
I verkligheten varierar spänningen från punkt till punkt i ett material. För att beskriva detta i tre dimensioner används spänningstensorer. Den vanligaste är Cauchy-spänningstensor som är en 3×3-matris innehållande tre normalkomponenter och tre (oberoende) skjuvkomponenter. Genom att lösa tensorens egenvärdesproblem får man huvudspänningar (principal stresses) och deras riktningar — dessa är de normalkomponenter som uppstår när koordinatsystemet är vridet så att skjuvkomponenterna blir noll.
Materialbeteende och spänning–töjning
Relationen mellan spänning och deformation (töjning) är central i materiallära. För linjärt elastiska material gäller Hookes lag i enkel form: σ = E ε, där E är elasticitetsmodulen och ε är normaltöjningen. Ett materialprov på en spännings–töjning-kurva visar vanligen:
- ett elastiskt område där deformationen är reversibel,
- en flytgräns (yield) där plastisk deformation börjar,
- en ultimat brottgräns och slutligen brott.
Vid konstruktion tas ofta säkerhetsfaktorer i beaktande för att undvika plastisk deformation eller brott under servicebelastningar.
Enheter och vanliga storheter
- SI-enhet: pascal (Pa) = N/m². I praktiken används ofta MPa (megapascal) eller GPa (gigapascal) för materialdata.
- Imperial: psi (pounds per square inch).
- Dimension: samma som tryck (ML⁻¹T⁻² i dimensionsanalys).
Mätning och praktiska aspekter
- Mätmetoder: strain gauges (töjningsgivare), extensometrar, digital bildkorrelation (DIC) och fotoelasticitet används för att bestämma spänningar eller töjningar i prov och komponenter.
- Olikformig fördelning: i många konstruktioner är spänningsfältet inte homogent. Geometriska övergångar, hål och skarpa hörn ger upphov till spänningskoncentrationer där lokala spänningar blir betydligt högre än genomsnittet.
- Fatique: upprepad lastning kan orsaka spricktillväxt och brott vid spänningsnivåer under materialets hållfasthetsgräns; därför dimensionerar man ofta för utmattningsstyrka.
Exempel
En enkel, vanlig beräkning: en stång med tvärsnittsarea A belastas med en axialkraft F. Genomsnittlig normalspänning är σ = F/A. Om F = 10 kN och A = 20 mm² blir σ = 10 000 N / 20·10⁻⁶ m² = 500·10⁶ N/m² = 500 MPa.
Sammanfattning
Spänning beskriver de inre krafter per ytenhet i ett material och är avgörande för att förstå hur konstruktioner bär upp laster. Begreppet finns i flera former (normal-, skjuv-, böj- och torsionsspänning), kan beskrivas lokalt med hjälp av spänningstensorer och mäts i pascal. Kännedom om spänningsfördelningar, materialets spännings–töjningsbeteende och spänningskoncentrationer är grundläggande för säker och effektiv konstruktion och materialval.
Figur 1.4 Skjuvspänning i en prismatisk stång. Spännings- eller kraftfördelningen i stångens tvärsnitt är inte nödvändigtvis jämn. Trots detta kan en genomsnittlig skjuvspänning τ a v g {\displaystyle \tau _{\mathrm {avg} }\,\! }
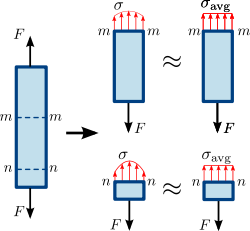
Figur 1.3 Normalspänning i en prismatisk stång (rak del med enhetlig tvärsnittsarea). Spännings- eller kraftfördelningen i stångens tvärsnitt är inte nödvändigtvis enhetlig. En genomsnittlig normalspänning σ a v g {\displaystyle \sigma _{\mathrm {avg} }\,\! }
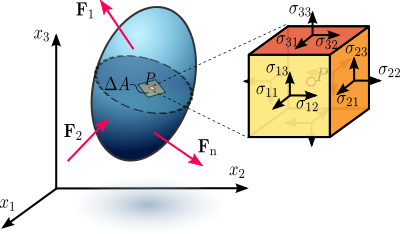
Figur 1.1 Spänningar i en belastad deformerbar materialkropp som antas vara ett kontinuum.
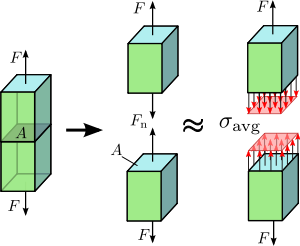
Figur 1.2 Axialspänning i en prismatisk stång som belastas axiellt.
Skjuvspänning
Mer information: Skjuvspänning
Enkla spänningar
I vissa situationer kan spänningen i ett objekt beskrivas med ett enda tal eller en enda vektor (ett tal och en riktning). Tre sådana enkla spänningssituationer är den enaxliga normalspänningen, den enkla skjuvspänningen och den isotropa normalspänningen.
Enaxial normalspänning
Dragspänning (eller spänning) är det spänningstillstånd som leder till expansion, det vill säga att längden på ett material tenderar att öka i dragriktningen. Materialets volym förblir konstant. När lika stora och motsatta krafter tillämpas på en kropp kallas spänningen till följd av denna kraft för dragspänning.
I ett enaxligt material ökar därför längden i dragspänningsriktningen och de andra två riktningarna minskar i storlek. I det uniaxiella spänningsmönstret induceras dragspänningen av dragkrafter. Dragspänning är motsatsen till tryckspänning.
Konstruktionsdelar som är direkt spända är linor, jordankare, spikar, bultar osv. Balkar som utsätts för böjmoment kan innehålla dragspänningar samt tryckspänningar och/eller skjuvspänningar.
Dragspänningen kan ökas till dess att draghållfasthet uppnås, dvs. gränsvärdet för spänningen.
Spänningar i endimensionella kroppar
Alla verkliga föremål befinner sig i ett tredimensionellt rum. Om två dimensioner är mycket stora eller mycket små jämfört med de andra kan föremålet dock modelleras som endimensionellt. Detta förenklar den matematiska modelleringen av objektet. Endimensionella objekt är t.ex. en trådbit som belastas i ändarna och betraktas från sidan, och en metallplåt som belastas på framsidan och betraktas på nära håll och genom tvärsnittet.
Relaterade sidor
- Spänning
- Böjning
Frågor och svar
F: Vad är stress?
S: Stress är den kraft per ytenhet på en kropp som tenderar att få den att ändra form. Det är ett mått på de inre krafterna i en kropp mellan dess partiklar och är den genomsnittliga kraften per ytenhet som en partikel i en kropp utövar på en intilliggande partikel över en tänkt yta som skiljer dem åt.
F: Hur påverkar yttre krafter spänningen?
S: Yttre krafter är antingen ytkrafter eller kroppskrafter, och de orsakar deformation av kroppens form som kan leda till permanent formförändring eller strukturellt brott om materialet inte är tillräckligt starkt.
F: Vad är formeln för enaxlig normalspänning?
S: Formeln för enaxlig normalspänning är σ = F/A, där σ är spänningen, F är kraften och A är ytan. I SI-enheter mäts kraften i Newton och ytan i kvadratmeter, vilket innebär att spänningen är Newton per kvadratmeter (N/m2). Det finns dock en egen SI-enhet för spänning som kallas pascal (Pa), som är lika med 1 N/m2. I imperiala enheter skulle den mätas i pundkraft per kvadrattum (psi).
F: Vad antar kontinuumsmekaniken om kraft?
S: Klassiska modeller av kontinuumsmekanik utgår från en genomsnittlig kraft och inkluderar inte geometriska faktorer på ett korrekt sätt - vilket innebär att de inte tar hänsyn till hur geometrin påverkar hur energin byggs upp vid applicering av yttre kraft.
F: Hur kan olika modeller ge olika resultat när man tittar på deformation av materia och fasta kroppar?
S: Olika modeller betraktar deformation av materia och fasta kroppar på olika sätt eftersom materiens och fasta kroppars egenskaper är tredimensionella - så varje metod tar hänsyn till olika aspekter, vilket kan leda till varierande resultat.
F: Hur behandlar kontinuumsmekaniken belastade deformerbara kroppar?
S: Kontinuumsmekaniken behandlar belastade deformerbara kroppar som kontinua - vilket innebär att de inre krafterna fördelas kontinuerligt inom materialkroppens volym i stället för att koncentreras till vissa punkter som i klassiska modeller.
Sök