Logaritmisk spiral
En logaritmisk spiral, ekviangulär spiral eller tillväxtspiral är en speciell typ av spiralkurva som ofta förekommer i naturen. Den logaritmiska spiralen beskrevs först av Descartes och undersöktes senare ingående av Jakob Bernoulli, som kallade den Spira mirabilis, "den underbara spiralen".
Spiralgalaxernas armar har ofta formen av en logaritmisk spiral, här Whirlpool-galaxen.
Ett lågtrycksområde över Island visar ett ungefär logaritmiskt spiralmönster.
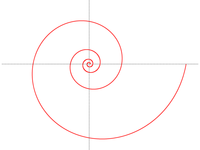
Logaritmisk spiral (stigning 10°)
Utsnitt av ett nautilusskal som visar kamrarna i en ungefär logaritmisk spiral.
Definition
I polära koordinater (r, θ) kan kurvan skrivas som följande
r = a e b θ {\displaystyle r=ae^{b\theta }\,} 
eller
θ = 1 b ln ( r / a ) , {\displaystyle \theta ={\frac {1}{b}}}\ln(r/a),} 
därav namnet "logaritmisk". I parametrisk form är kurvan
x ( t ) = r cos ( t ) = a e b t cos ( t ) {\displaystyle x(t)=r\cos(t)=ae^{bt}\cos(t)\,} 
y ( t ) = r sin ( t ) = a e b t sin ( t ) {\displaystyle y(t)=r\sin(t)=ae^{bt}\sin(t)\,} 
med de reella talen a och b.
Spiralen har egenskapen att vinkeln ɸ mellan tangenten och radiallinjen i punkten (r,θ) är konstant. Denna egenskap kan uttryckas i differentialgeometriska termer som
arccos ⟨ r ( θ ) , r ′ ( θ ) ⟩ ‖ r ( θ ) ‖ ‖ r ′ ( θ ) ‖ = arctan 1 b = ϕ , {\displaystyle \arccos {\frac {\langle \mathbf {r} (\theta ),\mathbf {r} '(\theta )\rangle }{\\|\\mathbf {r} (\theta )\|\|\mathbf {r} '(\theta )\|}}}=\arctan {\frac {1}{b}}}=\phi ,} 
Derivatan r'(θ) är proportionell mot parametern b. Med andra ord styr den hur "tätt" och i vilken riktning spiralen kretsar. I extremfallet att b = 0 (ɸ = π/2) blir spiralen en cirkel med radien a. Omvänt, i gränsen att b närmar sig oändligheten (ɸ → 0) tenderar spiralen mot en rät linje. Komplementet till ɸ kallas för stigning.
Spira mirabilis och Jakob Bernoulli
Spira mirabilis, latin för "mirakulös spiral", är ett annat namn på den logaritmiska spiralen. Även om denna kurva redan hade fått ett namn av andra matematiker, fick den namnet "mirakulös" eller "underbar" spiral av Jakob Bernoulli, eftersom han fascinerades av en av dess unika matematiska egenskaper: spiralens storlek ökar, men formen förblir densamma med varje tillagd kurva. Kanske på grund av denna egenskap har spira mirabilis utvecklats i naturen och ses i vissa levande varelser, till exempel i nautilusskal och solrosskallar. Jakob Bernoulli ville ha formen på sin gravsten, men av misstag placerades en arkimedisk spiral där i stället.
Logaritmiska spiraler i naturen
I flera naturfenomen kan man hitta kurvor som ligger nära logaritmiska spiraler. Här följer några exempel och skäl:
- En hök närmar sig sitt byte. Den skarpaste sikten är i en vinkel mot flygriktningen; denna vinkel är samma som spiralens stigning.
- En insekts närmande till en ljuskälla. De är vana vid att ljuskällan står i en konstant vinkel mot deras flygbana. Vanligtvis är solen den enda ljuskällan och om man flyger åt det hållet blir det en praktiskt taget rak linje.
- Spiralgalaxernas armar. Vår egen galax, Vintergatan, tros ha fyra större spiralarmar, som var och en är ungefär en logaritmisk spiral med en stigning på cirka 12 grader, vilket är en ovanligt liten stigningsvinkel för en galax som Vintergatan. Generellt sett har spiralgalaxernas armar en lutningsvinkel på mellan 10 och 40 grader.
- Armarna på tropiska cykloner, t.ex. orkaner.
|
|
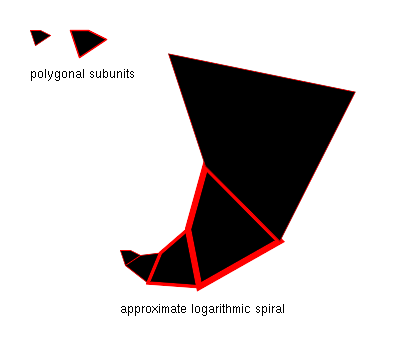
- Många biologiska strukturer, inklusive spindelväv och blötdjurens skal. I dessa fall är orsaken följande: Börja med en oregelbundet formad tvådimensionell figur F0 . Expandera F0 med en viss faktor för att få F1 , och placera F1 bredvid F0 , så att två sidor rör vid varandra. Utvidga nu F1 med samma faktor för att få F2 , och placera den bredvid F1 som tidigare. Genom att upprepa detta får man fram en ungefärlig logaritmisk spiral vars lutning bestäms av expansionsfaktorn och vinkeln med vilken figurerna placerades bredvid varandra. Detta visas för polygonala figurer i den bifogade figuren.
