Multiplikation: definition, regler, egenskaper och exempel i matematik

Multiplikation: definition, regler, egenskaper och tydliga exempel — lär dig kommutativitet, visuella tolkningar och praktiska övningar för alla nivåer.

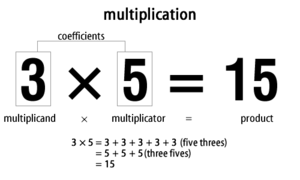
Multiplikation är en aritmetisk operation för att hitta produkten av två tal. Multiplikation är den tredje operationen i matematik efter addition som är den första, subtraktion som är den andra och sedan multiplikation.

Med naturliga tal anger det antalet brickor i en rektangel där ett av de två talen är lika med antalet brickor på ena sidan och det andra talet är lika med antalet brickor på den andra sidan.

Med verkliga tal anger den arean av en rektangel där det första talet är lika med storleken på den ena sidan och det andra talet är lika med storleken på den andra sidan.

Exempelvis är tre multiplicerat med fem summan av fem treor som adderas, eller summan av tre femmor. Detta kan skrivas ner som 3 × 5 = 15, eller uttalas som "tre gånger fem är lika med femton". Matematiker kallar de två tal som du vill multiplicera för "koefficienter" tillsammans, eller "multiplikand" och "multiplikator" var för sig. Multiplikand × multiplikator = produkt.

Multiplikation mellan tal sägs vara kommutativ - när talens ordning inte påverkar värdet av produkten. Detta gäller för heltal (hela tal), t.ex. 4 × 6 är detsamma som 6 × 4, och även för rationella tal (bråk), och för alla andra reella tal (som kan representeras som ett fält i den kontinuerliga linjen), och även för komplexa tal (som kan representeras som ett fält i planet). Det gäller inte för kvaternioner (tal som kan representeras som en ring i det fyrdimensionella rummet), vektorer eller matriser.

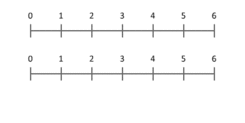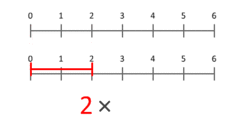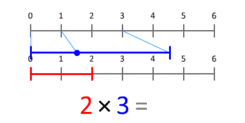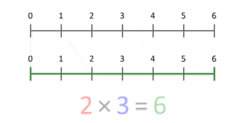
Definitionen av multiplikation som upprepad addition ger ett sätt att komma fram till en mängdteoretisk tolkning av multiplikation av kardinaltal. En mer korrekt tolkning är att se det som en skalning av storheter. Denna animation illustrerar hur 3 multipliceras med 2, vilket ger 6 som resultat. Lägg märke till att den blå pricken i det blå segmentet med längden 3 placeras på position 1, och att det blå segmentet skalas så att denna prick placeras i slutet av det röda segmentet med längden 2. Vid multiplikation med valfritt X kommer den blå pricken alltid att börja vid 1 och sluta vid X. Detta fungerar även för X som är mindre än 1, eller negativt.

Motsatsen till multiplikation är division.

Grundläggande begrepp och notation

Multiplikation skrivs på flera olika sätt:

• Med kryss: 3 × 5 = 15
• Med punkt: 3 · 5 = 15
• Genom att skriva talen intill varandra (vanligt i algebra): ab = a·b

Ett multiplikationstecken används ofta inom aritmetik medan i algebra och mer avancerade uttryck används prick eller inget tecken för att undvika förväxling med bokstaven x.

Viktiga regler och egenskaper

• Kommutativitet: a · b = b · a (gäller för tal i fält som reella och komplexa tal).
• Associativitet: (a · b) · c = a · (b · c). Detta gör att man kan gruppera faktorer fritt.
• Distributivitet över addition: a · (b + c) = a·b + a·c. Distributiva lagen kopplar ihop multiplikation och addition.
• Identitetselement: 1 · a = a. Talet 1 är multiplikativt identitetselement.
• Nollregeln: 0 · a = 0. Multiplicerar man med noll blir produkten noll.
• Teckenregler (för heltal): positiv · positiv = positiv; negativ · negativ = positiv; negativ · positiv = negativ.
• Invers: För varje icke-noll tal a finns ett multiplikativt invers a^{-1} så att a·a^{-1} = 1. (För reella tal a^{-1} = 1/a.)

Multiplikation för olika taltyper

Multiplikation fungerar något olika beroende på vilka typer av tal man multiplicerar:

• Naturliga tal: Tolkas ofta som upprepad addition eller som ett räkneproblem med rader och kolumner (rektangelmodell).
• Heltal: Samma regler som för naturliga tal gäller, men med teckenantaganden för negativa tal.
• Rationella tal (bråk): Multiplicera täljare med täljare och nämnare med nämnare: (a/b)·(c/d) = (a·c)/(b·d). Förkortning efteråt kan behövas.
• Reella tal: Kan tolkas som skalning av längder eller areor. Multiplikation av reella tal är kommutativ och distributiv.
• Komplexa tal: Multiplikation motsvarar både skalning och rotation i det komplexa planet.
• Matriser och vektorer: Matrismultiplikation är i allmänhet icke-kommutativ (AB ≠ BA i allmänhet). Skalär multiplikation (multiplicera en vektor eller matris med ett tal) följer de vanliga regelerna.

Geometrisk tolkning och skalning

En vanlig tolkning av multiplikation är area: om en rektangel har sidor med längder a och b så är arean a·b. En annan tolkning är skalning: att multiplicera en längd med ett tal betyder att skala längden med den faktorn. Denna syn förklarar varför multiplikation fungerar även för icke-heltal och negativa tal (skalningen kan bli mindre än 1 eller speglas).

Exempel och beräkningar

Några konkreta exempel:

• 3 × 5 = 15 (upprepad addition: 5 + 5 + 5 = 15 eller 3 + 3 + 3 + 3 + 3 = 15)
• (−2) × 4 = −8 och (−2) × (−3) = 6
• 0,5 × 4 = 2 (decimalmultiplikation: halvfaktor gånger 4)
• 2/3 × 9/4 = (2·9)/(3·4) = 18/12 = 3/2

För större tal används algoritmer som kolumnmetoden (långa multiplikation), partiella produkter eller moderna datoralgoritmer (t.ex. FFT-baserade metoder för mycket stora tal).

Multiplikationstabell och snabba strategier

En grundläggande färdighet är att kunna multiplikationstabellen upp till 10×10 eller 12×12. För snabb huvudräkning kan man använda strategier som:

• Faktorisera en faktor: 25 × 12 = 25 × (4 × 3) = (25 × 4) × 3 = 100 × 3 = 300.
• Använda närmevärden och justera: 19 × 6 = (20 − 1) × 6 = 120 − 6 = 114.
• Dubbla och halvera: 25 × 16 = (25 × 2) × 8 = 50 × 8 = 400.

Multiplikation och enheter

När man multiplicerar mätetal multipliceras även enheterna: 3 m × 4 m = 12 m² (area). Vid multiplikation av olika enheter kombineras de (t.ex. hastighet = distans/tid), och dimensionell analys kan användas för att kontrollera om ett uttryck är enhetligt.

Kopplingar till andra operationer

Multiplikation är nära kopplad till:

• Additionsupprepadning: Grundläggande definition för naturliga tal.
• Potenser: a^n = a·a·...·a (n faktorer).
• Rotuttryck: rötter är inversa operationer till potenser, som i sin tur bygger på multiplikation.
• Division: Division är den inversa operationen: om a·b = c så är b = c/a (för a ≠ 0).

Vanliga misstag att undvika

• Glöm inte teckenreglerna för negativa tal.
• För ihop något fel vid multiplikation av bråk — multiplicera diagonalt (täljare med täljare, nämnare med nämnare).
• Blandning av symboler: i algebra kan a×b ofta skrivas ab förkortat.

Sammanfattning

Multiplikation är en grundläggande matematisk operation med många tolkningar: upprepad addition, area, skalning eller kombination av storheter. Den följer centrala lagar som kommutativitet, associativitet och distributivitet och används överallt — från enkel huvudräkning till avancerad algebra och analys. Förståelse av dess regler, tolkningar och metoder för beräkning gör det lättare att lösa praktiska och teoretiska problem.

Frågor och svar

F: Vad är multiplikation?

F: Vad kallas de två tal som ska multipliceras?

F: Är multiplikation kommutativ?

F: Hur kan vi tolka multiplikation av kardinal tal?

F: Hur representerar man tre multiplicerat med fem?

F: Vad är motsatsen till multiplikation?

Sök med bokstav