Harmoniska serien

Historia

Det faktum att den harmoniska serien divergerar bevisades för första gången på 1300-talet av Nicole Oresme, men glömdes bort. På 1600-talet gavs bevis av Pietro Mengoli, Johann Bernoulli och Jacob Bernoulli.

Harmoniska sekvenser har använts av arkitekter. Under barocken använde arkitekter dem i proportionerna i planritningar, fasader och i förhållandet mellan arkitektoniska detaljer i kyrkor och palats.

 

Divergens

Det finns flera välkända bevis för divergensen hos de harmoniska serierna. Några av dem anges nedan.

Jämförelsetest

Ett sätt att bevisa divergens är att jämföra den harmoniska serien med en annan divergent serie, där varje nämnare ersätts med den näst största potensen av två:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&1+{\frac {1}{2}}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}}}

Varje term i den harmoniska serien är större än eller lika med motsvarande term i den andra serien, och därför måste summan av den harmoniska serien vara större än eller lika med summan av den andra serien. Summan av den andra serien är dock oändlig:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}}\!+\!{\frac {1}{8}}}\!+\!{\frac {1}{8}}}\right)+\left({\frac {1}{16}}}\!+\!\cdots \!+\!{\frac {1}{16}}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}}+{\frac {1}{2}}}+{\frac {1}{2}}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}

Av jämförelsetestet följer att summan av de harmoniska serierna också måste vara oändlig. Mer exakt bevisar jämförelsen ovan att

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}}

för varje positivt heltal k.

Detta bevis, som lades fram av Nicole Oresme omkring 1350, anses vara en höjdpunkt i den medeltida matematiken. Det är fortfarande ett standardbevis som lärs ut i matematikkurser i dag.

Integral test

Det är möjligt att bevisa att den harmoniska serien divergerar genom att jämföra dess summa med ett olämpligt integral. Tänk på det arrangemang av rektanglar som visas i figuren till höger. Varje rektangel är 1 enhet bred och

1/n enheter, så den totala arean av det oändliga antalet rektanglar är summan av de harmoniska serierna:

arean av rektanglar = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}}=1+{\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{4}}}+{\frac {1}{5}}+\cdots }

Den totala arean under kurvan y =

1/x från 1 till oändligheten ges av ett divergent olämpligt integral:

area under kurvan = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{area under}}\{\text{kurva}}\end{array}}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .}

Eftersom denna yta är helt och hållet innesluten i rektanglarna måste rektanglarnas totala yta också vara oändlig. Detta bevisar att

∑ n = 1 k 1 n > ∫ 1 k + 1 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}}>\int _{1}^{k+1}{\frac {1}{x}}}\,dx=\ln(k+1).}

Generaliseringen av detta argument är känd som integraltestet.

 
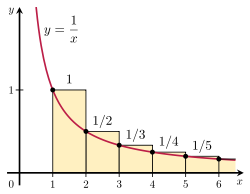
Illustration av integralförsöket.  

Divergenshastighet

Den harmoniska serien divergerar mycket långsamt. Till exempel är summan av de 10 första termerna på⁴³ mindre än 100. Detta beror på att seriens partiella summor har logaritmisk tillväxt. I synnerhet,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}

där γ är Euler-Mascheroni-konstanten och ε_k ~

1/2k som närmar sig 0 när k blir oändligt. Leonhard Euler bevisade både detta och att den summa som endast omfattar de reciproka primtalen av primtalen också divergerar, det vill säga:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}}={\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{5}}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .}
 

Partiella summor

De trettio första harmoniska talen
n	Partiell summa av den harmoniska serien, Hn
	uttryckt som en bråkdel		decimal	relativ storlek
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

De ändliga partiella summorna av divergerande harmoniska serier,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}},}

kallas harmoniska tal.

Skillnaden mellan H_n och ln n konvergerar mot Euler-Mascheroni-konstanten. Skillnaden mellan två harmoniska tal är aldrig ett heltal. Inga harmoniska tal är heltal, utom H₁ = 1.

 

Relaterade serier

Växlande harmoniska serier

Serien

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots }

är känd som den växlande harmoniska serien. Denna serie konvergerar med hjälp av testet för alternerande serier. I synnerhet är summan lika med den naturliga logaritmen av 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}}+{\frac {1}{3}}}-{\frac {1}{4}}}+{\frac {1}{5}}}-\cdots =\ln 2.}

Den alternerande harmoniska serien är visserligen villkorligt konvergent, men inte absolut konvergent: om termerna i serien systematisk omorganiseras blir summan i allmänhet annorlunda och, beroende på omorganiseringen, eventuellt till och med oändlig.

Formeln för den alternerande harmoniska serien är ett specialfall av Mercator-serien, Taylor-serien för den naturliga logaritmen.

En relaterad serie kan härledas från Taylor-serien för arktangenten:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}}=1-{\frac {1}{3}}}+{\frac {1}{5}}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}}.}

Detta kallas Leibniz-serien.

Allmänna harmoniska serier

Den allmänna harmoniska serien har formen

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},}

där a ≠ 0 och b är verkliga tal, och

b/a är inte noll eller ett negativt heltal.

Genom gränsjämförelsetestet med de harmoniska serierna avviker också alla allmänna harmoniska serier.

p-serien

En generalisering av den harmoniska serien är p-serien (eller hyperharmoniska serien), definierad som

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}

för varje verkligt tal p. När p = 1 är p-serien den harmoniska serien, som divergerar. Antingen integraltestet eller Cauchys kondensationstest visar att p-serien konvergerar för alla p > 1 (i så fall kallas den överharmonisk serie) och divergerar för alla p ≤ 1. Om p > 1 är summan av p-serien ζ(p), dvs. Riemanns zeta-funktion utvärderad vid p.

Problemet med att hitta summan för p = 2 kallas Baselproblemet; Leonhard Euler visade att det är

π² /6. Värdet av summan för p = 3 kallas Apérys konstant, eftersom Roger Apéry bevisade att det är ett irrationellt tal.

ln-serien

Relaterad till p-serien är ln-serien, definierad som

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}

för alla positiva reella tal p. Detta kan visas med hjälp av integraltestet att det divergerar för p ≤ 1 men konvergerar för alla p > 1.

φ-serien

För varje konvex realvärdesfunktion φ som är sådan att

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}}},}

serien

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}}\right)}

är konvergent.

Slumpmässiga harmoniska serier

Den slumpmässiga harmoniska serien

∑ n = 1 ∞ s n n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}}{n}},}

där s_n är oberoende, identiskt fördelade slumpmässiga variabler som tar värdena +1 och -1 med samma sannolikhet.

1/2, är ett välkänt exempel inom sannolikhetsteorin på en serie slumpvariabler som konvergerar med sannolikheten 1. Denna konvergens är en enkel följd av antingen Kolmogorovs sats om tre serier eller den närbesläktade Kolmogorovs maximala ojämlikhet. Byron Schmuland vid University of Alberta undersökte ytterligare egenskaperna hos den slumpmässiga harmoniska serien och visade att den konvergerande serien är en slumpvariabel med vissa intressanta egenskaper. Särskilt sannolikhetstäthetsfunktionen för denna slumpvariabel utvärderad vid +2 eller -2 antar värdet 0,124999999999999999999999999999999999999999999999764 ..., vilket skiljer sig från 1/8 med mindre än 10⁻⁴² . I Schmulands artikel förklaras varför denna sannolikhet ligger så nära, men inte exakt, 1/8. Det exakta värdet av denna sannolikhet ges av den oändliga cosinusproduktintegralen C₂ dividerad med π.

Utarmade harmoniska serier

Den utarmade harmoniska serien där alla termer där siffran 9 förekommer någonstans i nämnaren tas bort kan visas konvergera och dess värde är mindre än 80. Faktum är att när alla termer som innehåller en viss sifferföljd (i vilken bas som helst) tas bort konvergerar serien.

 
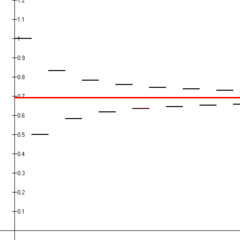
De första fjorton partiella summorna av den alternerande harmoniska serien (svarta linjesegment) som konvergerar mot den naturliga logaritmen av 2 (röd linje).  

Applikationer

Den harmoniska serien kan vara kontraintuitiv. Detta beror på att det är en divergent serie trots att seriens termer blir mindre och går mot noll. Divergensen hos den harmoniska serien är källan till vissa paradoxer.

• "Masken på gummibandet". Anta att en mask kryper längs ett oändligt elastiskt enmeters gummiband samtidigt som gummibandet sträcks jämnt. Om masken rör sig 1 centimeter per minut och bandet sträcks ut 1 meter per minut, kommer masken då någonsin att nå slutet av gummibandet? Svaret är kontraintuitivt nog "ja", för efter n minuter är förhållandet mellan den sträcka som masken har färdats och gummibandets totala längd följande

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}}\sum _{k=1}^{n}{\frac {1}{k}}.}

Eftersom serien blir godtyckligt stor när n blir större måste detta förhållande till slut överstiga 1, vilket innebär att masken når slutet av gummibandet. Det värde på n vid vilket detta inträffar måste dock vara extremt stort: ungefär e¹⁰⁰ , ett tal som överstiger 10⁴³ minuter (10³⁷ år). Även om den harmoniska serien divergerar gör den det mycket långsamt.

• Jeepproblemet handlar om hur mycket bränsle en bil med begränsad bränslekapacitet behöver för att korsa en öken och lämna bränslespillror längs vägen. Den sträcka som bilen kan köra med en given mängd bränsle är relaterad till de partiella summorna av den harmoniska serien, som växer logaritmiskt. Bränslebehovet ökar alltså exponentiellt med den önskade sträckan.

• Blockstaplingsproblemet: Med en samling identiska dominobrickor är det möjligt att stapla dem vid kanten av ett bord så att de hänger över bordskanten utan att falla. Det kontraintuitiva resultatet är att de kan staplas på ett sätt som gör att överhänget blir hur stort som helst. Det vill säga, förutsatt att det finns tillräckligt många dominobrickor.

• En simmare som går snabbare varje gång han eller hon rör vid bassängväggen. Simmaren börjar korsa en 10-metersbassäng med en hastighet av 2 m/s, och med varje korsning läggs ytterligare 2 m/s till hastigheten. I teorin är simmarens hastighet obegränsad, men antalet överfarter av bassängen som krävs för att uppnå den hastigheten blir mycket stort. För att uppnå ljusets hastighet (om man bortser från den speciella relativitetsteorin) måste simmaren till exempel korsa bassängen 150 miljoner gånger. I motsats till detta stora antal beror den tid som behövs för att nå en viss hastighet på summan av serierna vid ett visst antal bassängövergångar:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}}\sum _{k=1}^{n}{\frac {1}{k}}.}

Om man räknar ut summan visar det sig att den tid som krävs för att nå ljusets hastighet endast är 97 sekunder.

 
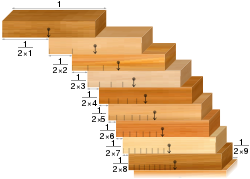
Problemet med blockstapling: block som är uppställda enligt den harmoniska serien överbryggar klyftor av valfri bredd.  

Relaterade sidor

• Harmonisk utveckling
• Förteckning över summor av reciproker