Linjär funktion

I grundläggande matematik är en linjär funktion en funktion vars graf är en rät linje i två dimensioner (se bilder). Ett exempel är: y=2x-1. I högre matematik avser en linjär funktion ofta en linjär avbildning.

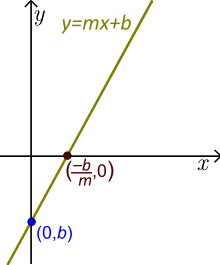
Linjär funktion (Linjen här är generisk. Den är snedställd så att m≠0. Se exempel med faktiska värden för m och b nedan.)

Grundläggande egenskaper

Formellt sett är en linjär funktion en funktion f(x):R→R så att grafen för f är en linje. Detta innebär att f:s domän eller ingång är ett reellt tal R och att f:s område eller utgång också är ett reellt tal R. Vanligtvis skriver vi y(x) eller bara y i stället för f(x). Den formella förklaringen betyder alltså:

Vi matar in eller ersätter ett reellt tal x i den linjära funktionen.
den linjära funktionen ger ett reellt tal y eller ger ett reellt tal y och
Alla dessa punkter (x,y) bildar en linje.

Det finns tre huvudformer för att skriva linjära funktioner: lutningsintercept, standard och parametrisk.

Form med lutning och intercept

Den explicita formen för en linjär funktion är y ( x ) = m x + b {\displaystyle y(x)=mx+b} $y(x)=mx+b$ eller y = m x + b {\displaystyle y=mx+b} $y=mx+b$ . Denna form har två variabler x och у och två konstanter m och b.

Bokstäverna m och b är konstanter. Innan vi arbetar med en linjär funktion ersätter vi m och b med verkliga tal.
Bokstäverna x och y är variabler.

Variabeln x kallas den oberoende variabeln eller argumentet. Alla reella tal x kan matas in eller ersättas i en linjär funktion. Funktionen ger sedan ut motsvarande värde för y.
Variabeln y kallas den beroende variabeln. Det är det värde som produceras efter att x har ersatts med ett värde som används som ingångsvärde.

Horisontella linjer ingår. Linjen är horisontell om och endast om m=0. Då har vi bara y=b. Eftersom b är ett reellt tal är detta en konstant funktion. En konstant funktion är alltså också en linjär funktion.
Vertikala linjer ingår aldrig eftersom en vertikal linje inte är en funktion. En vertikal linje klarar inte testet för vertikala linjer. (En vertikal linje definieras av ekvationen: x=b där b är ett reellt tal).
Snedstreckade linjer är inkluderade. Linjen är sned om och endast om m≠0.

Formen för den sluttande interceptet är unik. Ett annat värde på m eller ett annat värde på b ger en annan linje.
En linjär funktion är en polynomisk funktion av första eller nollgrad i en variabel х .
Den konstanta termen är b. Om vi sätter in x=0 i funktionen får vi y=b. Så talet b är y-interceptet och linjen korsar у-axeln i punkten (0,b).
Om m≠0 är talet^–b / _mx-interceptet eller roten eller noll och (^–b /_m ,0) är den punkt där linjen korsar х-axeln. Här är funktionens värde noll.
Koefficienten m till x kallas linjens lutning eller gradient. För varje linje är talet m en konstant och därför är lutningen konstant för hela linjen. Lutningen bestämmer både linjens riktning och branthet. Riktning och branthet kallas förändringshastighet. Förändringshastigheten är alltså m och den är konstant för varje linje.

Tecknet på m bestämmer riktningen. Om m>0 är den linjära funktionen ökande; om m<0 är funktionen minskande.
Absolutvärdet av m bestämmer brantheten. Om |m|<1 är sluttningen mjuk, om |m|>1 är sluttningen brant.
Om lutningen på en linje är m och (х,у) är en punkt på linjen, måste vi också ha punkten (х+1, y+m) på linjen.

Exempel: y=-2x+4. Lutningen är m= -2 och y-interceptet är b=4 eller punkten (0,4). Genom att ersätta y=0 och lösa för x får vi 0=-2x+4 eller x=2. Så x=2 är roten till denna linjära funktion och punkten (2,0) är x-interceptet. Eftersom lutningen är m = -2 är linjen fallande. Eftersom |-2|=2>1 är minskningen relativt brant. För varje förändring av х med 1 (till höger) ändras värdet av у med -2 (sjunker).

Grafen för en linje bestäms av två punkter. För att grafera en linjär funktion kan vi sätta in två olika värden för x i funktionen och lösa de motsvarande y-värdena. Vi ritar dessa två punkter. Med hjälp av ett linjal drar vi linjen genom dessa två punkter och förlänger den förbi båda punkterna.

Exempel: y=-2x+4. Genom att ersätta x=0 får vi y=4 (detta är y-interceptet) och därmed punkten (0,4). Genom att ersätta x=1 får vi y=2 och därmed punkten (1,2). Rita upp dessa punkter och dra linjen. (Lägg märke till att den andra punkten ligger 1 till höger och 2 nedåt från den första punkten. Som vi sa i exemplet ovan sker detta eftersom lutningen är m= -2).

En linjär funktion som inte är en konstant funktion är en bijektion. Den ger ut varje verkligt tal (surjektion) för exakt ett ingångsvärde (injektion).

Exempel: y= -x+2. Anta att y= -1. Vi ersätter y= -1 och får: -1= -'x+2 eller x=3. Detta är den enda lösningen. Vi kan göra detta för vilket y-värde som helst.

Standardformulär

A x + B y = C , B ≠ 0 {\displaystyle Ax+By=C,\,B\neq 0} $Ax+By=C,\,B\neq 0$ .

Standardformen har 2 variabler x och у och 3 konstanter A, B och C som ersätts med verkliga tal innan man arbetar. Denna form används ofta i geometri och i system av linjära ekvationer.

Exempel: Den linjära funktionen 3x-2y=1 är i standardform. Konstanterna är A=3, B=-2 och C=1.

Denna form skrivs ibland som: A x + B y + C = 0 {\displaystyle Ax+By+C=0} $Ax+By+C=0$ . Så istället för att skriva 3x-2y=1 skriver vi den motsvarande ekvationen 3x-2y-1=0.
Konstanterna A, B och C är inte entydigt bestämda. Om vi multiplicerar dem med en faktor k ändras värdet på dessa konstanter, men linjen är fortfarande densamma.

Exempel: Linjerna 3x-2y=1 och 6x-4y=2 är sammanfallande (samma linje). Här är faktorn: k=2. Vi multiplicerade den första ekvationen med 2 för att få den andra ekvationen. Den unika formen för den här linjen är: y=1,5x-0,5 (lös båda ekvationerna för y).

Vektor-parametrisk form

Parametrisk form: { x ( t ) = x 1 + a 1 t y ( t ) = y 1 + a 2 t a 1 ≠ 0 , t ∈ R {\displaystyle \left\{{\begin{array}{*{20}{l}}{x(t)={x_{1}}}+{a_{1}}}t}\\\{y(t)={y_{1}}}+{a_{2}}t}\end{array}}}\right.\,{a_{1}\neq 0}\,,\,t\in \mathbb {R} } $\left\{{\begin{array}{*{20}{l}}{x(t)={x_{1}}+{a_{1}}t}\\{y(t)={y_{1}}+{a_{2}}t}\end{array}}\right.\,{a_{1}\neq 0}\,,\,t\in \mathbb {R}$ eller

Vektorform: X = ( x 1 , y 1 ) + t ( a 1 , a 2 ) {\displaystyle {\mathbf {X} }=({x_{1}}},{y_{1}}})+t({a_{1}}},{a_{2}})} } ${\mathbf {X} }=({x_{1}},{y_{1}})+t({a_{1}},{a_{2}})$ eller r ( t ) = < x 1 + a 1 t , y 1 + a 2 t > , a 1 ≠ 0 , t ∈ R {\displaystyle r(t)=\,<x_{1}+a_{1}t,\,y_{1}+a_{2}t>\,,\,{a_{1}\neq 0}\,,\,t\in \mathbb {R} } $r(t)=\,<x_{1}+a_{1}t,\,y_{1}+a_{2}t>\,,\,{a_{1}\neq 0}\,,\,t\in \mathbb {R}$ .

Den parametriska eller vektor- eller vektor-parametriska formen har 1 parameter t, 2 variabler x och у och 4 konstanter a₁ , a₂ , x₁ och y₁ . Koefficienterna a₁ , a₂ , x₁ och y₁ är inte entydigt bestämda. Linjen passerar genom punkterna А=(x₁ ,y₁ ) och B=(x₁ +a₁ ,y₁ +a₂ ), så om man tar andra punkter eller till och med bara byter ordning på punkterna får man olika konstanter för samma linje.
Parametern t är inte synlig i diagrammet.
Ingenjörer använder vanligtvis bokstaven t för parametern. Matematiker använder ofta den grekiska bokstaven λ.

Exempel: X=(-1,1)+t(2,3), t∈R är en linje i vektorform. Här: a₁ =2, a₂ =3, x₁ =-1 och x₂ =1. Linjen går genom punkterna (x₁ ,y₁ )=(-1,1) och (x₁ +a₁ ,y₁ +a₂ )=(1,4). Den motsvarande parametriska formen för denna linje är: x(t)= -1+2t, y(t)=1+3t. Den unika formen för denna linje är: y(x)=1,5x+2,5 (lös den första ekvationen för t och sätt in resultatet i den andra ekvationen).

Den vektorparametriska formen av en linje utvidgas naturligt till linjer i tredimensionella och högre rum. De andra formerna gör det inte.

Exempel: X=(-1,1,2)+t(2,3,-1), t∈R är en linje i det tredimensionella rummet. Linjen går genom punkterna (-1,1,2) och (1,4,1).

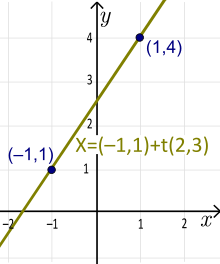
Vektorparametrisk form av en linje (icke unik). Den unika formen för lutning och intercept är y=1,5x+2,5.

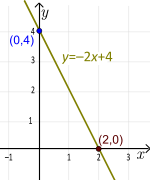
En linjes form med lutning och intercept (unik)

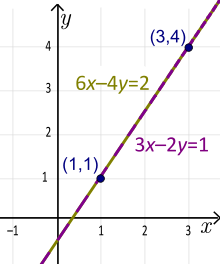
Standardform av en linje (icke unik). Den unika formen för lutning och intercept är y=1,5x-0,5.

Derivat av en linjär funktion

I det sammanhang där den definieras är derivatan av en funktion ett mått på hur snabbt funktionens värden förändras i förhållande till förändringen av ingångsvärdena. En linjär funktion har en konstant förändringstakt. Denna förändringshastighet är lutningen m. M är alltså derivatan. Detta skrivs ofta:

( m x + b ) ′ = m {\displaystyle (mx+b)^{\prime }=m} $(mx+b)^{\prime }=m$

Exempel: y= -2x+4. Här är m= -2 och y′= -2.

Linjär funktion vs. linjär ekvation

Ofta förväxlas termerna linjär ekvation och linjär funktion. Båda är polynomier. Ordet linjär i linjär ekvation betyder dock att alla termer med variabler är av första graden. (Ordet linjär i linjär funktion betyder att grafen är en linje.) En linjär ekvation kan ha 1, 2, 3 eller fler variabler. En linjär ekvation är alltså en linjär funktion endast om den har exakt 2 variabler. (En linjär ekvation med en variabel är en punkt på tallinjen och en linjär ekvation med tre variabler är ett plan i det tredimensionella rummet).

Notation

Många länder och discipliner använder olika bokstäver och ordningsföljder för de olika formerna.

I många länder skrivs en linjär funktion ofta som y = a x + b {\displaystyle y=ax+b} $y=ax+b$ där a är lutningen och b är y-interceptet.

Inom affärsverksamhet och ekonomi skrivs en linjär funktion ofta som y = a + b x {\displaystyle y=a+bx} $y=a+bx$ där a är y-interceptet och b är lutningen.

Relaterade sidor

Linje
Polynomiell
Konstant funktion
Kvadratisk ekvation
Linjär ekvation