AlegsaOnline.com

Venn-diagram: Förklaring, historia och praktiska exempel

Upptäck Venn-diagramets förklaring, historia och praktiska exempel — enkelt förklarat med visuella guider, tillämpningar i statistik, logik och datavetenskap.

Författare: Leandro Alegsa

16-11-2025

Ett Venn-diagram är ett diagram som visar det logiska förhållandet mellan mängder. De populariserades av John Venn på 1880-talet och används nu i stor utsträckning. De används för att lära ut elementär mängdteori och för att illustrera enkla mängdrelationer inom sannolikhet, logik, statistik, lingvistik och datavetenskap. I ett Venn-diagram används slutna kurvor på ett plan för att representera mängder. Ofta är dessa kurvor cirklar eller ellipser.

Liknande idéer hade föreslagits före Venn. Christian Weise 1712 (Nucleus Logicoe Wiesianoe) och Leonhard Euler (Letters to a German Princess) 1768, till exempel, hade liknande idéer. Idén populariserades av Venn i Symbolic Logic, kapitel V "Diagrammatic Representation", 1881.

Förklaring — vad visar ett Venn-diagram?

Ett Venn-diagram visar hur olika mängder förhåller sig till varandra genom överlappande områden. Varje sluten kurva (vanligtvis en cirkel) representerar en mängd. Om två cirklar överlappar finns det en del som tillhör båda mängderna — det är mängdernas snitt. Om cirklarna ligger bredvid varandra utan överlapp är mängderna disjunkta (ingen gemensam del).

Grundläggande mängdoperationer i Venn-diagram

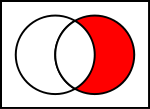
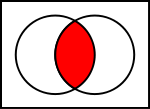
Snitt (A ∩ B): området där två cirklar överlappar.
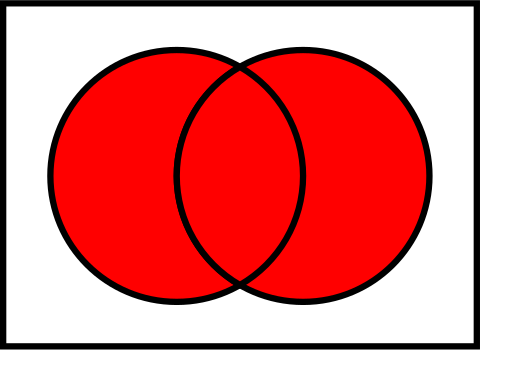
Union (A ∪ B): allt som ligger i minst en av cirklarna (båda + överlappet).
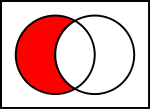
Skillnad (A \ B): delen av A som inte ligger i B.
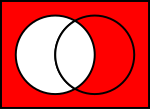
Komplement (A'): allt utanför A (i universum som diagrammet visar).

Praktiska exempel

Två mängder (enkelt exempel):

Låt A = {1,2,3,4} och B = {3,4,5}. I ett Venn-diagram är A och B två cirklar som överlappar i {3,4}. Då är A ∩ B = {3,4}, A ∪ B = {1,2,3,4,5} och A \ B = {1,2}.

Tremängdsdiagram (vanligt i undervisning):

Tre cirklar delar planet i sju icke-tomma regioner (utom om vissa regioner är tomma): tre områden som tillhör endast en av mängderna, tre områden som är snittet av par av mängder, och ett område som är snittet av alla tre. Dessa används ofta för att illustrera mer komplexa relationer och logiska kombinationer.

Tillämpningar

Sannolikhet: för att visa relationer mellan händelser och räkna sannolikheter. Exempel: P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
Logik: för att illustrera satslogiska relationer och mängdrelationer.
Dataanalys och statistik: för att jämföra grupper, hitta överlappningar i kundsegment, svar på enkätfrågor med flera svarsalternativ med mera.
Undervisning: som visuellt hjälpmedel för att förklara mängder och operationer.

Historia och skillnad mot Euler-diagram

Idén att använda områden för att representera mängder går tillbaka före John Venn — till exempel Christian Weise och Leonhard Euler. Det som Venn gjorde var att systematiskt konstruera diagram som visar alla möjliga logiska relationer mellan en given mängd av mängder (även om vissa relationer i praktiken är tomma). Det är skillnaden mot Euler-diagram, som bara visar de relationer som faktiskt finns: om ett område är tomt visas det helt enkelt inte. Ett Venn-diagram visar alltid alla tänkbara regioner för de ingående mängderna.

Hur man ritar ett Venn-diagram — enkla steg

Bestäm antalet mängder (2 eller 3 är vanligast för handritning).
Rita en cirkel för varje mängd så att de överlappar i de regioner du vill visa.
Markera eller skriv i de olika regionerna de element eller sannolikheter som hör dit.
Använd färger eller mönster för att tydliggöra överlapp och skillnader.

Tips: För mer än tre mängder behöver man ofta använda andra former än cirklar eller använda datorverktyg för att rita korrekta Venn-diagram. Cirklar räcker normalt bara för upp till tre mängder om man vill ha de klassiska symmetriska figurerna.

Begränsningar och variationer

Venn-diagram blir snabbt svåra att tolka visuellt när antalet mängder ökar (>3). För många mängder krävs komplexa kurvor eller alternativa visualiseringar.
Felaktig skala eller placering kan ge intryck av relationer som inte finns — var därför noggrann med etiketter och förklarande text.
Det finns generaliserade konstruktioner (icke-cirkulära Venn-diagram) som kan representera fler mängder men de blir visuellt mer komplicerade.

Sammanfattning

Ett Venn-diagram är ett enkelt, visuellt sätt att visa hur mängder relaterar till varandra. Det är pedagogiskt användbart i många ämnen som matematik, sannolikhet, logik och datavetenskap. För två och tre mängder fungerar cirklar utmärkt; för fler mängder krävs andra tekniker eller noggrant ritade kurvor. Skillnaden mot Euler-diagram är att Venn visar alla teoretiskt möjliga regioner, även om vissa är tomma i verkligheten.

Glasfönster i Cambridge, där John Venn studerade. Det visar ett Venn-diagram.

Exempel

I följande exempel används två uppsättningar, A och B, som här representeras som färgade cirklar. Den orange cirkeln, uppsättning A, representerar alla levande varelser som är tvåbenta. Den blå cirkeln, uppsättning B, representerar de levande varelser som kan flyga. Varje enskild typ av varelse kan föreställas som en punkt någonstans i diagrammet. Levande varelser som både kan flyga och har två ben - till exempel papegojor - ingår i båda uppsättningarna och motsvarar därför punkter i det område där de blå och orange cirklarna överlappar varandra. Det området innehåller alla sådana (och endast) sådana levande varelser.

Människor och pingviner är tvåbenta och befinner sig därför i den orangea cirkeln, men eftersom de inte kan flyga, befinner de sig i den vänstra delen av den orangea cirkeln, där den inte överlappar den blå cirkeln. Myggor har sex ben och kan flyga, så punkten för myggor ligger i den del av den blå cirkeln som inte överlappar den orange cirkeln. Varelser som inte har två ben och inte kan flyga (t.ex. valar och spindlar) skulle alla representeras av punkter utanför båda cirklarna.

Den kombinerade ytan av mängderna A och B kallas union av A och B, betecknad med A ∪ B. Unionen innehåller i detta fall alla levande varelser som antingen är tvåbenta eller som kan flyga (eller båda). Området i både A och B, där de två uppsättningarna överlappar varandra, kallas skärningspunkten mellan A och B, betecknad med A ∩ B. Till exempel är skärningspunkten mellan de två uppsättningarna inte tom, eftersom det finns punkter som representerar varelser som finns i både den orange och den blå cirkeln.

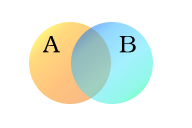
Uppsättningar A (varelser med två ben) och B (varelser som kan flyga).

Venndiagram för vanliga operationer på mängder

I illustrationerna nedan visar den vänstra cirkeln uppsättning A {\displaystyle A} $A$ och den högra cirkeln visar uppsättning B {\displaystyle B} $B$ . Resultaten av operationerna visas som färgade områden.

Relaterade sidor

Exklusiv disjunktion
Inkluderande disjunktion

Frågor och svar

Fråga: Vad är ett Venn-diagram?

S: Ett Venn-diagram är ett diagram som visar det logiska förhållandet mellan mängder. Det använder slutna kurvor som ritas på ett plan, vanligtvis cirklar eller ellipser, för att representera mängder.

Fråga: Vem populariserade Venn-diagrammen?

S: John Venn populariserade Venn-diagrammen på 1880-talet.

F: Vad används de till?

S: De används för att lära ut elementär mängdteori och illustrera enkla mängdförhållanden inom sannolikhet, logik, statistik, lingvistik och datavetenskap.

F: Vem föreslog liknande idéer före John Venn?

S: Christian Weise föreslog liknande idéer 1712 med sin Nucleus Logicoe Wiesianoe och Leonhard Euler föreslog dem i Letters to a German Princess 1768.

F: När publicerade John Venn Symbolic Logic?

S: John Venn publicerade Symbolic Logic år 1881.

F: I vilket kapitel i Symbolic Logic populariserades idén om ett Venn-diagram av John Venn?

S: Idén om ett Venn-diagram populariserades av John Venn i kapitel 5 "Diagrammatic Representation" i Symbolic Logic.

F: Hur representerades dessa idéer innan den moderna versionen av Venn-diagrammet uppfanns?

S: Innan den moderna versionen av V enn-diagrammet uppfanns representerades dessa idéer med hjälp av slutna kurvor som ritades på ett plan, t.ex. cirklar eller ellipser.