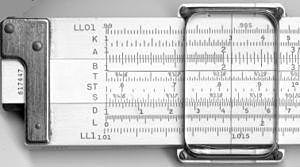
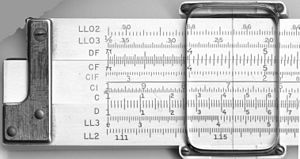
Räknesticka | mekanisk analog dator

Grundläggande begrepp

I sin mest grundläggande form använder räknestickan två logaritmiska skalor för att snabbt kunna multiplicera och dividera tal. Dessa vanliga operationer kan vara tidskrävande och felbenägna när de utförs på papper. Mer komplexa räknestickor möjliggör andra beräkningar, t.ex. kvadratrötter, exponentialer, logaritmer och trigonometriska funktioner.

Matematiska beräkningar görs genom att ett märke på den glidande mittremsan anpassas till ett märke på en av de fasta remsorna. Det relativa läget för andra märken kan sedan observeras. Siffror som är i linje med märkena ger det ungefärliga värdet av produkten, kvoten eller ett annat beräknat resultat.

Användaren bestämmer var decimaltecknet ska placeras i resultatet, baserat på en mental uppskattning. Vetenskaplig notation används för att spåra decimalpunkten i mer formella beräkningar. Additions- och subtraktionssteg i en beräkning görs i allmänhet mentalt eller på papper, inte på räknestickan.

De flesta räknestickor har tre linjära remsor av samma längd. Remsorna är parallella och samverkande så att den mittersta remsan kan flyttas i längdled i förhållande till de andra två. De två yttre remsorna är fasta så att deras relativa positioner inte ändras.

Vissa räknestickor (duplexmodeller) har skalor på båda sidorna av räknestickan och räknestången, andra har skalor på en sida av de yttre stängerna och båda sidorna av räknestången, och ytterligare andra har skalor på bara en sida (simplexregler). En glidande markör med en vertikal linje används för att hitta motsvarande punkter på skalor som inte ligger bredvid varandra eller, i duplexmodeller, ligger på andra sidan av regeln. Markören kan också registrera ett mellanresultat på någon av skalorna.

 
Cursor på en räknesticka  

Användning av räknestickan för beräkning

Multiplikation

En logaritm omvandlar multiplikation och division till addition och subtraktion enligt reglerna log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} och log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} . Genom att flytta den övre skalan till höger med ett avstånd på log ( x ) {\displaystyle \log(x)} , genom att matcha den övre skalans början med etiketten x {\displaystyle x} på den nedre skalan, anpassas varje nummer y {\displaystyle y} , på positionen log ( y ) {\displaystyle \log(y)} på den övre skalan, med talet på positionen log ( x ) + log ( y ) {\displaystyle \log(x)+\log(y)} på den nedre skalan. Eftersom log ( x ) + log ( y ) = log ( x y ) {\displaystyle \log(x)+\log(y)=\log(xy)} ger denna position på den nedre skalan x y {\displaystyle xy} , produkten av x {\displaystyle x} och y {\displaystyle y} . För att till exempel beräkna 3 × 2 (representerat som 3*2 på en miniräknare) flyttas 1 på den övre skalan till 2 på den nedre skalan. Svaret, 6, avläses från den nedre skalan där 3 står på den övre skalan. I allmänhet flyttas 1 på den övre skalan till en faktor på den nedre skalan och svaret avläses på den nedre skalan där den andra faktorn är på den övre skalan.

Det kan hända att operationer går "utanför skalan"; till exempel visar diagrammet ovan att räknestickan inte har placerat 7:an på den övre skalan över något tal på den nedre skalan, så den ger inget svar på 2×7. I sådana fall kan användaren skjuta den övre skalan åt vänster tills dess högra index ligger i linje med 2, vilket i praktiken innebär att man multiplicerar med 0,2 i stället för med 2, som i illustrationen nedan:

Här måste användaren av räknestickan komma ihåg att justera decimaltecknet på lämpligt sätt för att korrigera det slutliga svaret. Vi ville hitta 2×7, men i stället beräknade vi 0,2×7=1,4. Det riktiga svaret är alltså inte 1,4 utan 14. Att ställa om räknesnurran är inte det enda sättet att hantera multiplikationer som skulle resultera i resultat utanför skalan, till exempel 2×7; några andra metoder är det:

• (1) Använd de dubbeldekadiska skalorna A och B.
• (2) Använd de vikta skalorna. I det här exemplet ställer du vänster 1 i C mittemot 2 i D. Flytta markören till 7 på CF och läs resultatet från DF.
• (3) Använd den inverterade CI-skalan. Placera 7 på CI-skalan ovanför 2 på D-skalan och läs sedan av resultatet på D-skalan under 1 på CI-skalan. Eftersom 1 förekommer på två ställen på CI-skalan kommer en av dem alltid att vara på skalan.
• (4) Använd både den inverterade CI-skalan och C-skalan. Ställ in 2 i CI på linje med 1 i D och läs av resultatet från D under 7 på C-skalan.

Metod 1 är lätt att förstå, men innebär en förlust av precision. Metod 3 har den fördelen att den endast omfattar två skalor.

Huvudgrupp

Illustrationen nedan visar beräkningen av 5,5/2. 2 på den övre skalan placeras över 5,5 på den nedre skalan. 1 på den övre skalan ligger över kvoten, 2,75. Det finns mer än en metod för att göra division, men den metod som presenteras här har den fördelen att slutresultatet inte kan vara utanför skalan, eftersom man kan välja att använda 1:an i båda ändarna.

Övriga verksamheter

Förutom de logaritmiska skalorna har vissa räknestickor andra matematiska funktioner kodade på andra extraskalor. De mest populära var trigonometriska, vanligen sinus och tangent, vanlig logaritm (log10) (för att ta logaritmen av ett värde på en multiplikatorskala), naturlig logaritm (ln) och exponentiella (e^x ) skalor. Vissa regler omfattar en pythagorisk skala, för att räkna ut trianglars sidor, och en skala för att räkna ut cirklar. Andra har skalor för att beräkna hyperboliska funktioner. På linjära regler är skalorna och deras märkning i hög grad standardiserade, och variationer förekommer vanligen endast när det gäller vilka skalor som ingår och i vilken ordning:

A, B	Logaritmiska skalor med två decennier, som används för att hitta kvadratrötter och kvadrater av tal.
C, D	Logaritmiska skalor med en enda decennium.
K	logaritmisk skala med tre decennier, som används för att hitta kubiska rötter och kuber av tal.
CF, DF	"Vikta" versioner av C- och D-skalorna som börjar från π i stället för från enhet; dessa är praktiska i två fall. För det första när användaren gissar att en produkt kommer att ligga nära 10 men inte är säker på om den kommer att vara något mindre eller något mer än 10, undviker de vikta skalorna möjligheten att gå utanför skalan. För det andra förenklas multiplikation eller division med π (vilket är vanligt i vetenskapliga och tekniska formler) genom att göra starten π i stället för kvadratroten av 10.
CI, DI, DIF	"Inverterade" skalor, från höger till vänster, används för att förenkla 1/x-steg.
S	används för att hitta sinus och cosinus på D-skalan.
T	används för att hitta tangenter och kotangenter på D- och DI-skalorna.
ST, SRT	Används för sinus och tangenter av små vinklar och konvertering av grader-radianer.
L	En linjär skala som används tillsammans med C- och D-skalorna för att hitta logaritmer och potenser av 10 i bas 10.
LLn	en uppsättning log-log-skalor som används för att hitta logaritmer och exponentialer för tal.
Ln	en linjär skala som används tillsammans med C- och D-skalorna för att hitta naturliga logaritmer (bas e) och e x {\displaystyle e^{x}}

 

Skalorna på fram- och baksidan av en K&E 4081-3 räknesticka.

Den binära räknestickan som tillverkades av Gilson 1931 utförde en addition och subtraktion begränsad till bråk.

Rötter och befogenheter

Det finns skalor med en decennieskala (C och D), två decennier (A och B) och tre decennier (K). För att beräkna x 2 {\displaystyle x^{2}} , till exempel, lokalisera x på D-skalan och avläs dess kvadrat på A-skalan. Om man vänder på denna process kan man hitta kvadratrötter, och på samma sätt för potenserna 3, 1/3, 2/3 och 3/2. Försiktighet måste iakttas när basen, x, hittas på mer än ett ställe på sin skala. Det finns till exempel två nior på Askalan; för att hitta kvadratroten av nio använder man den första nian; den andra nian ger kvadratroten av 90.

För x y {\displaystyle x^{y}} problem, använd LL-skalorna. När flera LL-skalor finns, använd den med x på den. Först anpassar du den vänstra 1:an på C-skalan till x på LL-skalan. Hitta sedan y på C-skalan och gå ner till LL-skalan med x på den. Den skalan visar svaret. Om y är "utanför skalan", lokalisera x y / 2 {\displaystyle x^{y/2}} och kvadrera det med hjälp av A- och B-skalorna enligt beskrivningen ovan.

Trigonometri

Skalorna S, T och ST används för trigonometriska funktioner och multipler av trigonometriska funktioner, för vinklar i grader. Många räknestickor har sina S-, T- och ST-skalor markerade med grader och minuter. Så kallade decitrigmodeller använder i stället decimalfraktioner av grader.

Logaritmer och exponentialer

Logaritmer och exponentialer i bas 10 hittas med hjälp av L-skalan, som är linjär. Vissa räknestickor har en Ln-skala, som är för bas e.

Ln-skalan uppfanns av Stephen B. Cohen, en elev i elfte klass, 1958. Den ursprungliga avsikten var att användaren skulle kunna välja en exponent x (i intervallet 0 till 2,3) på Ln-skalan och läsa e^x på C (eller D)-skalan och e^–x på CI (eller DI)-skalan. Pickett, Inc. fick exklusiva rättigheter till skalan. Senare skapade uppfinnaren en uppsättning "märken" på Ln-skalan för att utöka området bortom gränsen 2,3, men Pickett införde aldrig dessa märken i någon av sina räknestickor.

Addition och subtraktion

Slidegubbar används vanligtvis inte för addition och subtraktion, men det är ändå möjligt att göra det med hjälp av två olika tekniker.

Den första metoden för att utföra addition och subtraktion på C och D (eller andra jämförbara skalor) kräver att problemet omvandlas till ett divisionsproblem. Vid addition är kvoten av de två variablerna plus en gång divisorn lika med deras summa:

x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}

Vid subtraktion är kvoten av de två variablerna minus en gång divisorn lika med deras skillnad:

x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}}-1\right)y}

Denna metod liknar den additions- och subtraktionsteknik som används för elektroniska kretsar med hög hastighet och med det logaritmiska talsystemet i specialiserade datortillämpningar, t.ex. superdatorn Gravity Pipe (GRAPE) och dolda Markovmodeller.

Den andra metoden använder en glidande linjär L-skala som finns på vissa modeller. Addition och subtraktion utförs genom att föra markören till vänster (för subtraktion) eller höger (för addition) och sedan föra tillbaka markören till 0 för att läsa av resultatet.

 

Fysisk utformning

Linjära standardregler

Längden på räknestickan anges i form av skalornas nominella längd. Skalorna på de vanligaste "10-tums"-modellerna är faktiskt 25 cm långa, eftersom de tillverkades enligt metriska standarder, men vissa räknestickor har något längre skalor för att förenkla hanteringen när ett resultat har gått över. Fickregler är vanligtvis 5 tum. Modeller som var ett par meter långa såldes för att hängas upp i klassrum i undervisningssyfte. [1]

Vanligtvis markerar divisionerna en skala med en precision på två signifikanta siffror och användaren uppskattar den tredje siffran. Vissa avancerade räknestickor har förstorande markörer som gör markeringarna lättare att se. Sådana markörer kan effektivt fördubbla noggrannheten vid avläsningar, vilket gör att en 10-tums räknesticka kan fungera lika bra som en 20-tums.

Olika andra bekvämligheter har utvecklats. Trigonometriska skalor har ibland dubbla etiketter, svarta och röda, med kompletterande vinklar, den så kallade Darmstadt-stilen. Duplex räknestickor har ofta en del av skalorna på baksidan. Skalor är ofta "delade" för att få högre noggrannhet.

Specialiserade räknestickor uppfanns för olika former av teknik, affärsverksamhet och bankverksamhet. Dessa hade ofta vanliga beräkningar direkt uttryckta som särskilda skalor, till exempel låneberäkningar, optimala inköpskvantiteter eller särskilda tekniska ekvationer. Företaget Fisher Controls distribuerade till exempel en specialanpassad räknesticka som var anpassad för att lösa de ekvationer som används för att välja rätt storlek på industriella flödesregleringsventiler.

Cirkulära räknestickor

Cirkulära räknestickor finns i två grundtyper, en med två markörer (till vänster) och en annan med en rörlig skiva och en enda markör (till höger). Versionerna med två markörer utför multiplikation och division genom att upprätthålla en fast vinkel mellan markörerna när de roteras runt skivan. Versionen med en enda markör fungerar mer som en vanlig räknestickan genom lämplig justering av skalorna.

Den grundläggande fördelen med en cirkulär räknesticka är att verktygets längsta dimension minskas med en faktor 3 (dvs. med π). Till exempel skulle den yttre skalan på en 10 cm cirkulär räknesticka ha en maximal precision som motsvarar en vanlig räknesticka på 30 cm. Cirkulära räknestickor eliminerar också beräkningar "utanför skalan", eftersom skalorna är utformade för att "svepa runt"; de behöver aldrig omorienteras när resultaten är nära 1,0 - räknestickan är alltid i skala. För icke-cykliska icke-spiralformade skalor som S-, T- och LL-skalor förkortas dock skalans längd för att ge utrymme för ändmarginaler.

Cirkulära räknestickor är mekaniskt sett mer robusta och har en jämnare rörelse, men precisionen i skalans justering är känslig för centrering av en central pivot. En liten avvikelse på 0,1 mm från pivotens centrum kan i värsta fall resultera i ett 0,2 mm stort justeringsfel. Givaren förhindrar dock repor på ytan och markörerna. De mest exakta skalorna är placerade på de yttre ringarna. I stället för "delade" skalor använder avancerade cirkulära linjaler spiralskalor för mer komplexa operationer, t.ex. log-av-log-skalor. En 8-tums cirkulär linjal av högsta kvalitet hade en 50-tums spiralformad log-log-skala.

De största nackdelarna med cirkulära räknestickor är att det är svårt att lokalisera figurer längs en roterande skiva och att antalet skalor är begränsat. En annan nackdel med cirkulära räknestickor är att mindre viktiga skalor ligger närmare centrum och har lägre precision. De flesta eleverna lärde sig att använda räknestickor med linjära räknestickor och fann ingen anledning att byta.

En räknesticka som fortfarande används dagligen runt om i världen är E6B. Detta är en cirkulär räknesticka som först skapades på 1930-talet för flygplanspiloter för att underlätta dödräkning. Med hjälp av skalor som är tryckta på ramen hjälper den också till med diverse uppgifter som att omvandla tid, avstånd, hastighet och temperaturvärden, kompassfel och beräkna bränsleförbrukning. Det så kallade "prayer wheel" finns fortfarande tillgängligt i flygbutiker och används fortfarande flitigt. Även om GPS har minskat användningen av dödräkning för flygnavigering och handhållna räknare har tagit över många av dess funktioner, används E6B fortfarande i stor utsträckning som primär- eller reservutrustning och majoriteten av flygskolorna kräver att deras elever behärskar den i någon grad.

1952 introducerade det schweiziska klockföretaget Breitling ett pilotarmbandur med en integrerad cirkulär räknesticka som är specialiserad för flygberäkningar: Breitling Navitimer. Navitimer-ritstocken, som av Breitling kallades en "navigationsdator", hade funktioner för lufthastighet, stigningshastighet/tid/nedgång, flygtid, avstånd och bränsleförbrukning, samt funktioner för konvertering av kilometer-nautiska mil och bränslemängder på en gallon-liters liter.

Material

Traditionellt tillverkades räknestickor av hårt trä, t.ex. mahogny eller buxbom, med markörer av glas och metall. Minst ett högprecisionsinstrument var tillverkat av stål.

År 1895 började ett japanskt företag, Hemmi, att tillverka räknestickor av bambu, som hade fördelarna att vara formstabilt, starkt och naturligt självsmörjande. Dessa räknestickor av bambu introducerades i Sverige i september 1933 [2], och förmodligen bara lite tidigare i Tyskland. Skalorna var tillverkade av celluloid eller plast. Senare räknestickor var tillverkade av plast eller aluminium målat med plast. Senare markörer var av akryl eller polykarbonat som gled på teflonlager.

Alla premium räknestickor hade siffror och skalor ingraverade och sedan fyllda med färg eller annat harts. Målade eller tryckta räknestickor ansågs vara sämre eftersom markeringarna kunde slitas bort. Trots detta tillverkade Pickett, förmodligen Amerikas mest framgångsrika räknesticksföretag, alla tryckta skalor. Premium räknestickor hade smarta lås så att räknestickan inte skulle falla isär av misstag, och stötfångare för att skydda skalorna och markören från att gnugga på bordsskivor. Den rekommenderade rengöringsmetoden för graverade markeringar är att skrubba lätt med stålull. För målade räknestickor, och för den som inte har så bra hjärta, använd utspädd kommersiell fönsterputs och en mjuk trasa.

 
En enkel cirkulär räknesticka, tillverkad av Concise Co., Ltd., Tokyo, Japan, med endast invers, kvadratisk och kubisk skala. På baksidan finns en praktisk förteckning över 38 omvandlingsfaktorer för metriska och imperiala mått.  


Breitling Navitimer armbandsur med cirkulär räknesticka  


Pickett cirkulär räknesticka med två markörer. (4,25 tum / 10,9 cm diameter) Baksidan har ytterligare en skala och en markör.  

Historia

Slidregeln uppfanns omkring 1620-1630, kort efter att John Napier publicerade begreppet logaritm. Edmund Gunter från Oxford utvecklade en räkneapparat med en enda logaritmisk skala som, med ytterligare mätverktyg, kunde användas för att multiplicera och dividera. Den första beskrivningen av denna skala publicerades i Paris 1624 av Edmund Wingate (ca 1593-1656), en engelsk matematiker, i en bok med titeln "L'usage de la reigle de proportion en l'arithmetique & geometrie". Boken innehåller en dubbel skala som på ena sidan har en logaritmisk skala och på den andra sidan en tabellskala. År 1630 uppfann William Oughtred från Cambridge en cirkulär räknesticka, och 1632 kombinerade han två Gunter-reglar, som hölls ihop med händerna, till en anordning som känns igen som den moderna räknestickan. Liksom sin samtida i Cambridge, Isaac Newton, undervisade Oughtred sina idéer privat för sina studenter, men dröjde med att publicera dem, och liksom Newton blev han inblandad i en livlig kontrovers om prioritet, med sin tidigare student Richard Delamain och Wingates tidigare anspråk. Oughtreds idéer offentliggjordes först i publikationer av hans elev William Forster 1632 och 1653.

År 1677 skapade Henry Coggeshall en två fot lång vikbar måttstock för virkesmätning, kallad Coggeshalls räknesticka. Hans konstruktion och användningsområden för verktyget gav räknestickan ett syfte utanför den matematiska undersökningen.

År 1722 introducerade Warner två- och tredekadaskalorna och 1755 inkluderade Everard en inverterad skala; en räknesticka som innehåller alla dessa skalor brukar kallas för en "polyfas"-regel.

År 1815 uppfann Peter Roget räknestickan log log log, som innehöll en skala som visade logaritmens logaritm. Detta gjorde det möjligt för användaren att direkt utföra beräkningar med rötter och exponenter. Detta var särskilt användbart för bråkdelar av potenser.

Modern form

Den modernare formen skapades 1859 av den franske artillerilöjtnanten Amédée Mannheim, "som hade turen att få sin regel tillverkad av ett företag med nationellt rykte och att den antogs av det franska artilleriet". Det var vid den tiden, när ingenjörsyrket blev en erkänd yrkesverksamhet, som räknestickor började användas i stor utsträckning i Europa. De blev inte vanliga i USA förrän 1881, då Edwin Thacher introducerade en cylindrisk linjal där. Duplexregeln uppfanns av William Cox 1891 och tillverkades av Keuffel and Esser Co. i New York.

Astronomiskt arbete krävde också fina beräkningar, och i 1800-talets Tyskland användes en ca 2 meter lång räknesticka av stål vid ett observatorium. Den var försedd med ett mikroskop, vilket gav den en noggrannhet på sex decimaler.

Under andra världskriget använde bombardiers och navigatörer som behövde göra snabba beräkningar ofta specialiserade räknestickor. Ett kontor inom den amerikanska flottan utformade faktiskt ett generiskt "chassi" för räknestickor med en aluminiumkropp och en plastknapp i vilken celluloidkort (tryckta på båda sidor) kunde placeras för särskilda beräkningar. Processen uppfanns för att beräkna räckvidd, bränsleförbrukning och höjd för flygplan, och anpassades sedan till många andra ändamål.

Under 1950- och 1960-talen var räknestickan symbolen för ingenjörsyrket (på samma sätt som stetoskopet symboliserar läkaryrket). Den tyske raketforskaren Wernher von Braun tog med sig två Nestler räknestickor från 1930-talet när han flyttade till USA efter andra världskriget för att arbeta med det amerikanska rymdprogrammet. Under hela sitt liv använde han aldrig några andra räknemaskiner i fickan; räknestickor tjänade honom utmärkt för att göra snabba uppskattningar av raketkonstruktionsparametrar och andra siffror. Räkneexemplar av Pickett-märket i aluminium hade med sig fem Apollo-rymduppdrag, bland annat till månen, enligt reklam på Picketts N600-räknelådor [3].

Vissa ingenjörsstudenter och ingenjörer bar tio-tums räknestickor i bälteshölster, och till och med i mitten av 1970-talet var detta en vanlig syn på universiteten. Studenter kunde också ha en tio- eller tjugotums räknesticka för precisionsarbete hemma eller på kontoret, samtidigt som de bar med sig en femtums räknesticka i fickformat.

2004 utformade utbildningsforskarna David B. Sher och Dean C. Nataro en ny typ av räknestickan som bygger på prosthaphaeresis, en algoritm för snabb beräkning av produkter som är äldre än logaritmen. Det har dock inte funnits något praktiskt intresse för att konstruera en sådan utöver den första prototypen. [4] Arkiverad 2005-05-10 vid Wayback Machine

Minskning

Slåttermometerns betydelse började minska i takt med att elektroniska datorer, som var en ny men mycket sällsynt resurs på 1950-talet, blev allmänt tillgängliga för tekniska arbetare under 1960-talet. Införandet av Fortran 1957 gjorde datorer praktiska för att lösa matematiska problem av blygsam storlek. IBM introducerade en serie mer prisvärda datorer, IBM 650 (1954), IBM 1620 (1959) och IBM 1130 (1965), som riktade sig till den vetenskapliga och tekniska marknaden. John Kemenys programmeringsspråk BASIC (1964) gjorde det enkelt för studenter att använda datorer. Minidatorn DEC PDP-8 introducerades 1965.

Datorerna förändrade också beräkningens karaktär. Med räknestickor var det viktigt att arbeta med algebra för att få in uttryck i den mest beräkningsbara formen. Användare av räknestickor skulle helt enkelt approximera eller ta bort små termer för att förenkla beräkningen. Fortran gjorde det möjligt att skriva in komplicerade formler från läroböcker utan att behöva omformulera dem. Numerisk integration var ofta enklare än att försöka hitta lösningar i sluten form för svåra problem. Den unge ingenjören som bad om datortid för att lösa ett problem som kunde ha lösts med några svep på räknestickan blev en humoristisk kliché. Många datacenter hade en inramad räknesticka hängande på väggen med anteckningen "I nödfall, slå sönder glaset".

Ett annat steg mot att ersätta räknestickor med elektronik var utvecklingen av elektroniska räknemaskiner för vetenskaplig och teknisk användning. De första var Wang Laboratories LOCI-2, som lanserades 1965 och som använde logaritmer för multiplikation och division, och Hewlett-Packards HP-9100, som lanserades 1968. HP-9100 hade trigonometriska funktioner (sin, cos, tan) utöver exponentialer och logaritmer. Den använde CORDIC-algoritmen (coordinate rotation digital computer), som gör det möjligt att beräkna trigonometriska funktioner med hjälp av endast skift- och additionsoperationer. Denna metod underlättade utvecklingen av allt mindre vetenskapliga räknare.

Den sista spiken i kistan för räknestickan var lanseringen av vetenskapliga miniräknare i fickformat, varav Hewlett-Packards HP-35 från 1972 var den första. Sådana räknemaskiner blev kända som "räknemaskiner med räknestickan" eftersom de kunde utföra de flesta eller alla funktioner på en räknestickan. Med en kostnad på flera hundra dollar ansågs även detta vara dyrt för de flesta studenter. Medan professionella räknestickor också kunde vara ganska dyra, sålde apotek ofta enkla plastmodeller för under 20 dollar. Men 1975 kunde man köpa grundläggande elektroniska miniräknare med fyra funktioner för under 50 dollar. År 1976 erbjöd TI-30 en vetenskaplig miniräknare för under 25 dollar. Efter denna tid torkade marknaden för räknestickor snabbt ut i takt med att små vetenskapliga miniräknare blev överkomliga.

 
TI-30  


William Oughtred (1575-1660), uppfinnare av den cirkulära räknestickan.  


Ingenjör som använder en räknesticka. Observera mekanisk miniräknare i bakgrunden.  

Fördelar

• En räknesticka har en tendens att mildra felet med "falsk precision" och signifikans. Den typiska precisionen för en användare av en räknesticka är ungefär tre noggrannhetsklasser. Detta stämmer väl överens med de flesta uppgifter som kan användas för att skapa tekniska formler. När en modern fickräknare används kan precisionen visas med sju eller fler decimaler, medan resultaten i verkligheten aldrig kan vara mer exakta än de tillgängliga inmatningsuppgifterna.
• En räknesticka kräver en kontinuerlig uppskattning av storleksordningen på resultaten. På en räknesticka visar 1,5 × 30 (vilket är lika med 45) samma resultat som 1 500 000 × 0,03 (vilket är lika med 45 000). Det är upp till ingenjören att kontinuerligt fastställa resultatens rimlighet, något som kan gå förlorat när siffror slarvigt matas in i ett datorprogram eller en miniräknare.
• När du utför en sekvens av multiplikationer eller divisioner med samma tal kan svaret ofta bestämmas genom att bara titta på räknestickan utan någon manipulation. Detta kan vara särskilt användbart när man beräknar procentandelar, t.ex. för provresultat, eller när man jämför priser, t.ex. i dollar per kilogram. Flera beräkningar av hastighet-tid-avstånd kan utföras handsfree med en blick med en räknesticka.
• En räknesticka är inte beroende av elektricitet.
• En räknesticka är en teknik som är lätt att kopiera. Från ett givet exempel på en räknesticka kan fler konstrueras av en kompetent hantverkare från rudimentära material med hjälp av icke-industriella processer.
• Slide rules är mycket standardiserade, så du behöver inte lära dig något på nytt när du byter till en annan regel.
• Slide rules är mångsidiga och kan användas i situationer och miljöer där en mänsklig användare kan ha nedsatt fingerfärdighet (t.ex. på grund av att han/hon behöver skyddshandskar). Omvänt kan en miniräknare vara svår att använda i sådana situationer - det är osannolikt att en räknesticka leder till ett fel som liknar det fel som uppstår om man av misstag trycker på fel knapp på en miniräknare.
• Slidregler kan tillverkas av kartong eller papper. Många gratistavlor eller specialiserade beräkningsinstrument av kartong är i själva verket specialiserade linjära eller cirkulära räknestickor.

En fördel med att använda en räknestickan tillsammans med en elektronisk miniräknare är att man kan kontrollera en viktig beräkning genom att göra den på båda instrumenten.

 

Nackdelar

• Fel kan uppstå på grund av mekanisk oprecision.
• Beräkningar med hjälp av räknestickan är av begränsad precision på grund av deras analoga in- och utgångar. Omvänt har även blygsamma moderna miniräknare en upplösning på minst sex signifikanta siffror på grund av den diskreta numeriska inmatningen och de elektroniska operationerna med flytande punkter.

 

Relaterade sidor

• Abacus
• Logaritm